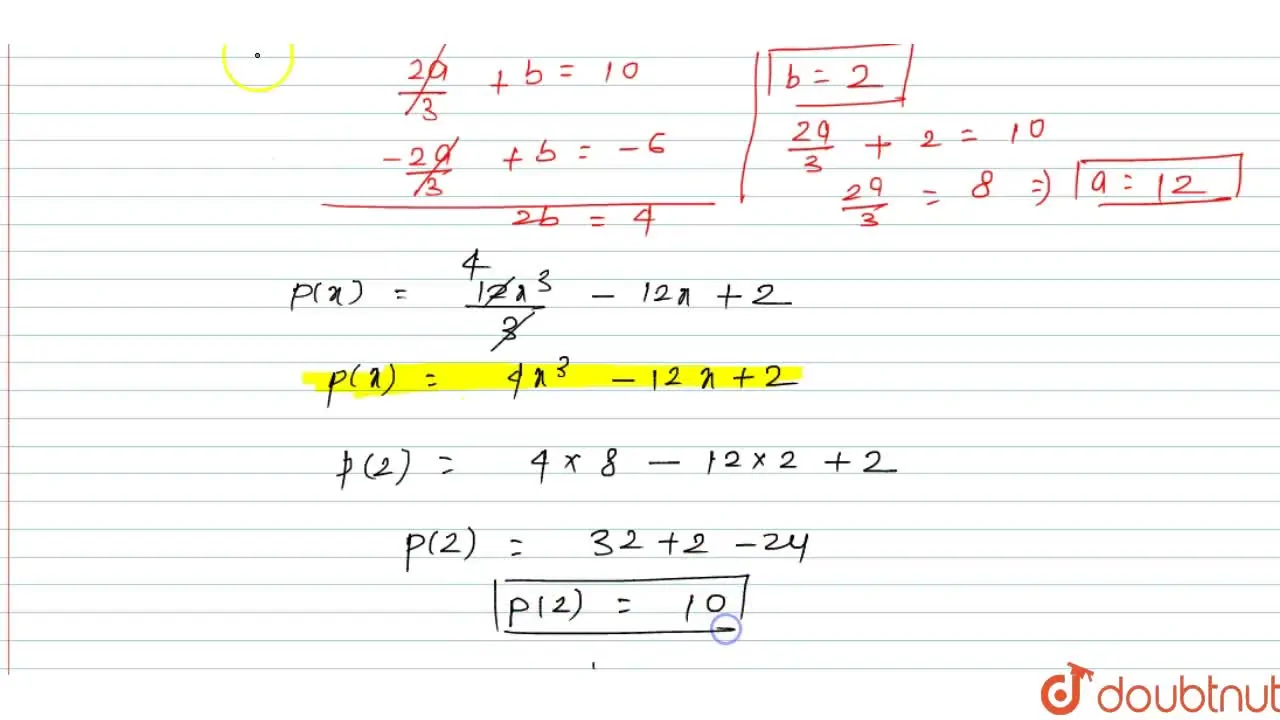P(x) be a polynomial of degree 3 satisfying P(-1) =10 , P(1) =-6 and p(x) has maxima at x = -1 and p(x) has minima at x=1 then The value of P(2) is (a) -15 (b) -16 (c) -17 (d) -22 (c) -17 (d) -22
-15
-16
-17
-22
The correct Answer is:3
P(x) is polynomial of degree 3
Given p(x) has minima at x=1
∴p(x)=a(x−1)
∴p(x)=a(x22−x)+b
Given p(x) has maximum at x =-1
∴p(−1)=a(x22−x)+b
Given p(x) has maxima at x =-1
∴b=−32a
∴p(x)=a(x36−(x23x)+C
Given p(-1)=10
∴a(−16−12+321)+C=10
∴5a+6c=60
∴p(1)=a(16−12−32)+c=−6
solving (1) alnd (2) we get
a=6 an c=5
∴p(x)=x3−3x2−9x+5
∴p(2)=8−12−18+5=−17
p(x)=3x2−6x−9
∴p(1)=3−6=−12
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type14videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension Type2videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
P(x) be a polynomial of degree 3 satisfying P(-1) =10 , P(1) =-6 and p(x) has maxima at x = -1 and p(x) has minima at x=1 then The value of P(1) is
View SolutionIf p(x) is a polynomial of degree 3 satisfying p(−1)=10,p(1)=−6andp(x) has maxima at x=−1andp'(x) has minima at x=1, find the distance between the local maxima and local minima of the curve.
View SolutionIf P(x)=x3−1 then the value of P(1)+P(−1) is
View SolutionConsider a polynomial P(x) of the least degree that has a maximum equal to 6 at x=1 and a minimum equal to 2 at x=3. Then the value of P(2)+P(0)−7 is
View SolutionIf P(x) is polynomial of degree 4 such than P(−1)=P(1)=5andP(−2)=P(0)=P(2)=2 find the maximum vaue of P (x).
View Solutionp(x) be a polynomial of degree at most 5 which leaves remainder - 1 and 1 upon division by (x−1)3 and (x+1)3respectively, the number of real roots of P(x)=0 is (a) 1 (b) 3 (c) 5 (d)2
View SolutionIf P(x) is a polynomial of the least degree that has a maximum equal to 6 at x=1, and a minimum equalto 2 at x=3,then ∫10P(x)dx equals:
View SolutionLet P(x) be a polynomial of degree 11 such that P(x)=1x+1 for x=0,1,2,3,….11. The value of P(12) is.
View SolutionLet p(x) be a real polynomial of least degree which has a local maximum at x=1 and a local minimum at x=3. If p(1)=6andp(3)=2, then p′(0) is_____
View SolutionLet p(x) be a real polynomial of least degree which has a local maximum at x=1 and a local minimum at x=3. If p(1)=6andp(3)=2, then p′(0) is_____
View Solution