Two runner A and B start at the origin and run along positive x axis ,with B running three times as fast as A. An obsever, standeing one unit above the origin , keeps A and B in view.Then the maximum angle theta of sight between the observer's view of A and B is
π/8
π/6
π/3
π/4
The correct Answer is:2
To solve the problem step by step, we can follow these instructions:
Step 1: Define Variables
Let the speed of runner A be vA. Then, the speed of runner B, who runs three times as fast, will be vB=3vA.
Step 2: Distance Traveled by Runners
At any time t:
- The distance traveled by runner A is x=vAt.
- The distance traveled by runner B is 3x=3vAt.
Step 3: Set Up the Coordinate System
We can represent the positions of the runners in a coordinate system:
- Runner A's position at time t is (x,0).
- Runner B's position at time t is (3x,0).
- The observer is located at point O(0,1).
Step 4: Calculate Angles of Sight
We need to find the angles of sight from the observer to each runner:
- For runner A, the angle θ1:
tan(θ1)=yx=1x
- For runner B, the angle θ2:
tan(θ2)=y3x=13x
Step 5: Find the Angle Between the Lines of Sight
The angle θ between the lines of sight to runners A and B can be expressed as:
tan(θ)=tan(θ2−θ1)=tan(θ2)−tan(θ1)1+tan(θ1)tan(θ2)
Step 6: Substitute the Values
Substituting the values of tan(θ1) and tan(θ2):
tan(θ)=13x−1x1+(1x)(13x)
This simplifies to:
tan(θ)=1−33x1+13x2=−23x1+13x2=−23x+1x
Step 7: Maximize the Angle
To find the maximum value of tan(θ), we need to maximize:
y=−23x+1x
We can differentiate this with respect to x and set the derivative to zero to find critical points.
Step 8: Differentiate and Solve
Differentiating y:
dydx=ddx(−23x+1x)
Using the quotient rule, we find:
dydx=0⋅(3x+1x)−(−2)(3−1x2)(3x+1x)2
Setting the numerator equal to zero gives:
2(3−1x2)=0⟹3=1x2⟹x2=13⟹x=1√3
Step 9: Determine the Maximum Angle
Substituting x=1√3 back into the expression for tan(θ):
tan(θ)=2√33+3=2√36=√33
Thus, the maximum angle θ is:
θ=tan−1(√33)=π6 radians=30∘
Final Answer
The maximum angle θ of sight between the observer's view of A and B is 30∘.
---
Let the speed of runner A be vA. Then, the speed of runner B, who runs three times as fast, will be vB=3vA.
At any time t:
- The distance traveled by runner A is x=vAt.
- The distance traveled by runner B is 3x=3vAt.
We can represent the positions of the runners in a coordinate system:
- Runner A's position at time t is (x,0).
- Runner B's position at time t is (3x,0).
- The observer is located at point O(0,1).
We need to find the angles of sight from the observer to each runner:
- For runner A, the angle θ1:
tan(θ1)=yx=1x
- For runner B, the angle θ2:
tan(θ2)=y3x=13x
The angle θ between the lines of sight to runners A and B can be expressed as:
tan(θ)=tan(θ2−θ1)=tan(θ2)−tan(θ1)1+tan(θ1)tan(θ2)
Substituting the values of tan(θ1) and tan(θ2):
tan(θ)=13x−1x1+(1x)(13x)
This simplifies to:
tan(θ)=1−33x1+13x2=−23x1+13x2=−23x+1x
To find the maximum value of tan(θ), we need to maximize:
y=−23x+1x
We can differentiate this with respect to x and set the derivative to zero to find critical points.
Differentiating y:
dydx=ddx(−23x+1x)
Using the quotient rule, we find:
dydx=0⋅(3x+1x)−(−2)(3−1x2)(3x+1x)2
Setting the numerator equal to zero gives:
2(3−1x2)=0⟹3=1x2⟹x2=13⟹x=1√3
Substituting x=1√3 back into the expression for tan(θ):
tan(θ)=2√33+3=2√36=√33
Thus, the maximum angle θ is:
θ=tan−1(√33)=π6 radians=30∘
The maximum angle θ of sight between the observer's view of A and B is 30∘.
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type
48 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type
24 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.7
5 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type
46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
Two particles A and B start from the origin along x-axis. Velocity time graph of both particles are shown in the figure. During the given time interval, the maximum separation between the particles is
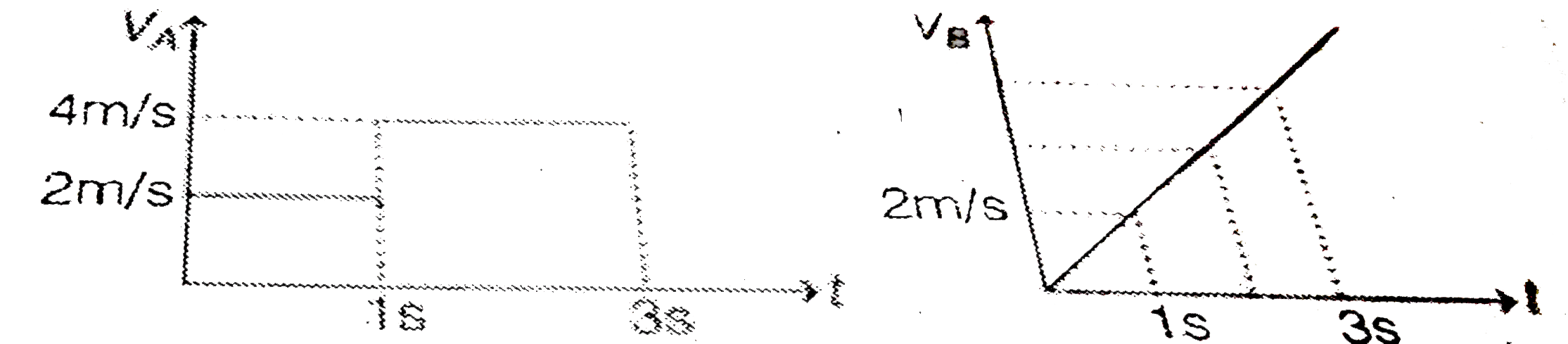
View SolutionIn rectangle OABC, point O is the origin, OA=10 units along x-axis and AB=8 units. Find the co-ordinates of vertices A,B and C.
View SolutionTwo persons A and B are standing at the origin and 210 meter away from the origin along the y-axis, respectively. A starts to move along x axis with acceleration 3.2m/s2 and thereafter with the same retardation and comes to rest after moving 320 m B moves with a constant velocity and catches A in 15 s. The speed of B is 10n3m/s. Find the value of n.
View SolutionTwo paricles A and B start at the origin O and travel in opposite directions along the circular path at constant speeds vA=0.7ms−1 and vB=1.0ms−1, respectively.
Determine the time when they collide and the magnitude of the acceleration of B just before this happens.

View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View SolutionA particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume tha the particle is at origin at t= 0).
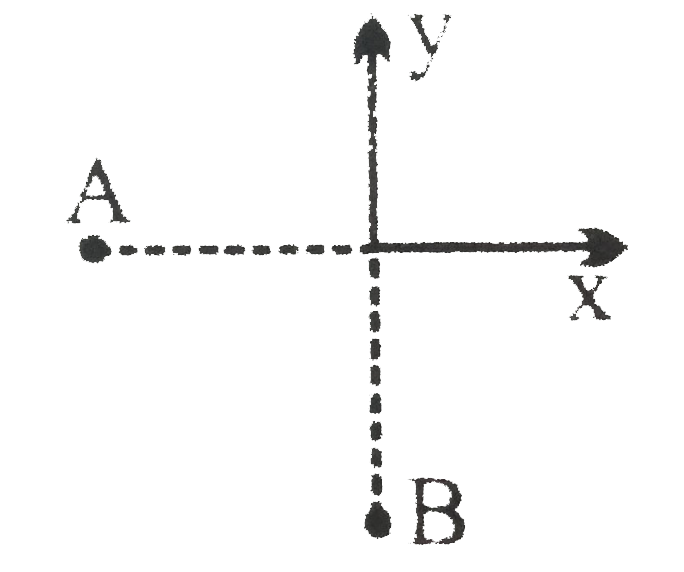
View SolutionTwo bodies A and B are moving along y-axis and x -axis as shown. Find the minimum distance between A and B is subsequent motion (in m)

View SolutionParticles A and B are moving with constant velocities along x and y axis respectively, the graph of separation between them with time is
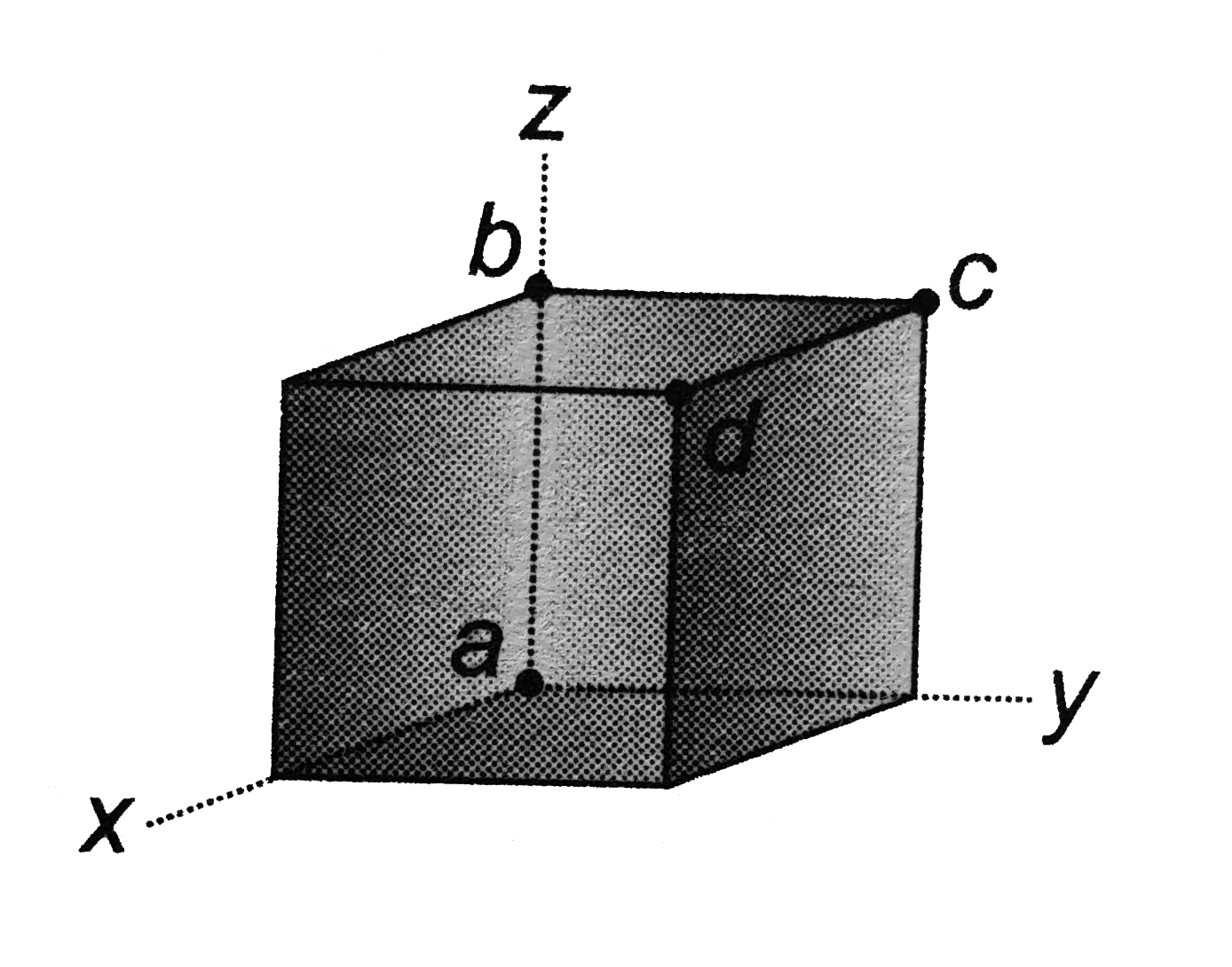
View SolutionA cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
View SolutionIf →a and →b are two unit vectors and θ is the angle between them, then the unit vector along the angular bisector of →a and →b will be given by
View Solution
