f:R→R,f(x) is differentiable such that f(f(x))=k(x5+x),k≠0). Then f(x) is always increasing (b) decreasing either increasing or decreasing non-monotonic
increasing
decreasing on [−1/2,∞]
either increasing or decreasing
non monotonic
The correct Answer is:3
f(f(x))=k(x5+x)orf'(f(x))f'(x)=k(5x4+1)
Thus f(x) is always increasing or decreasing as k(5x4+1) is eitehr always negative or positive .
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Multiple correct answers type
Explore 48 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Numerical Value Type
Explore 24 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Concept Application Exercise 6.7
Explore 5 Videos
- METHODS OF DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:METHODS OF DIFFERENTIATIONExercise:Single Correct Answer Type
Explore 46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSExercise:Comprehension Type
Explore 6 Videos
Similar Questions
The function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionIf f(x)=xex(x−1), then f(x) is
View SolutionIf f(x)=xex(x−1) , then f(x) is
View SolutionThe function f(x)=x1+|x| is (a) strictly increasing (b) strictly decreasing (c) neither increasing nor decreasing (d) none of these
View SolutionState whether f(x)=tanx−x is increasing or decreasing its domain.
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
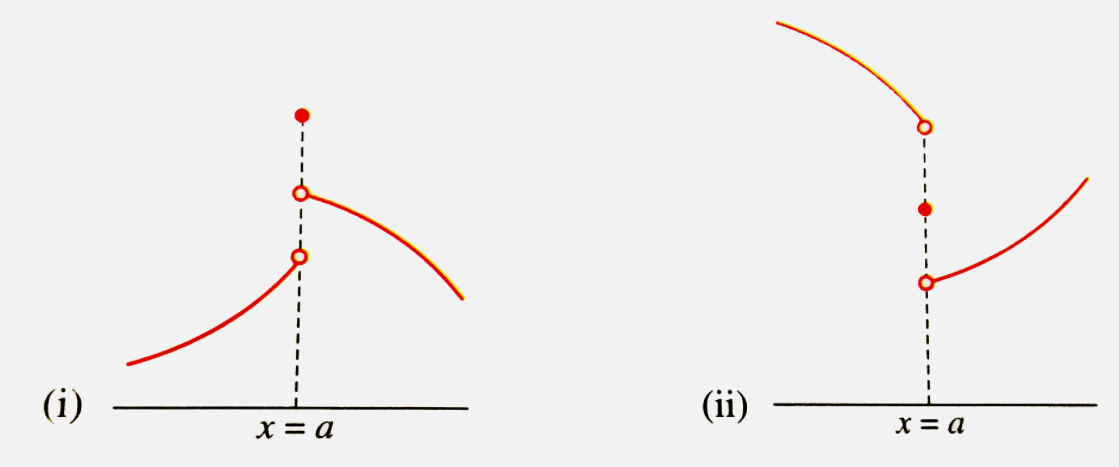
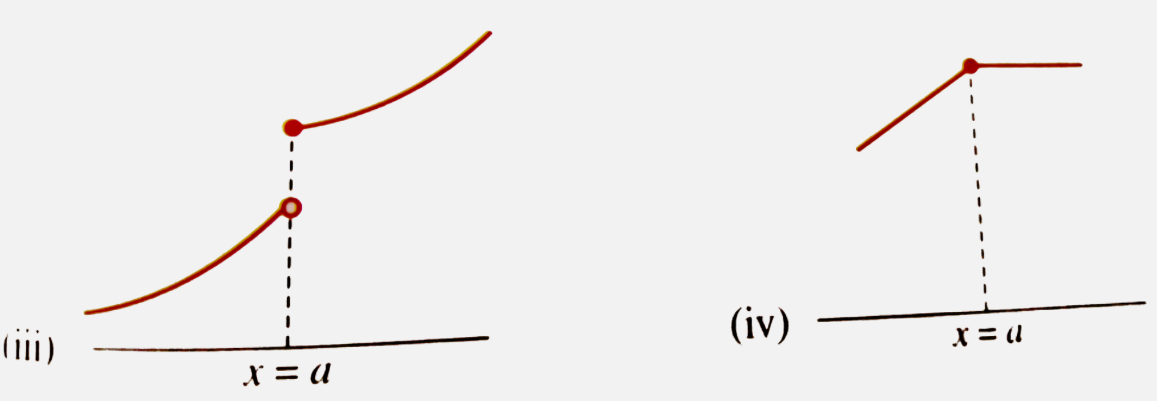
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing
View SolutionFind the interval for which f(x)=x−sinx is increasing or decreasing.
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing.
View SolutionShow that f(x)=cosx is decreasing function on (0,π), increasing in (−π,0) and neither increasing nor decreasing in (−π,π).
View Solution

