A regular square based pyramid is inscribed in a sphere of given radius R so that all vertices of the pyramid belong to the sphere. Find the greatest value of the volume of the pyramid.
The correct Answer is:6481r3
If we cut the sphere from the center along the diagonal of the square base we get the view show in figure

Let r be the radius of the spere Then
Height of the pyramid =r+r cosθ
Diagonal of the square base =2rsinθ
∴ side of the squre base =2rsinθ√2
Let v be the volume of the pyaramid .Then
V=13 (Area of the base xx Height)
=132rsinθ(√2)2×(r+rcosθ)
∴dVdθ=23r3[sin2θ(1+cosθ)−sin3θ]
=23r3[2sin2θcos2θ−sin3θ]
=23r3×sinθ(2cosθ+2cos2θ−sin2θ)
=23r3sinθ(3cos2θ+2cosθ−1)
=23r3sinθ(cosθ+1)(3cosθ−1)
For maximum or minimum values of v we must have dVdθ=0
or 3cosθ−1=0
cos θ=13
Hence V is maximum when cos θ=13andsinθ=2√23
The maximum value of V is given by
V=23r3×89(1+13)=6481r3
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Exercise
Explore 93 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Multiple correct answers type
Explore 48 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Concept Application Exercise 6.6
Explore 9 Videos
- METHODS OF DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:METHODS OF DIFFERENTIATIONExercise:Single Correct Answer Type
Explore 46 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSExercise:Comprehension Type
Explore 6 Videos
Similar Questions
A cone is inscribed in a sphere of radius 12 cm. If the volume of the cone is maximum, find its height.
View SolutionThe lateral edge of a regular rectangular pyramid is acmlong. The lateral edge makes an angle α with the plane of the base. Find the value of α for which the volume of the pyramid is greatest.
View Solution
Knowledge Check

A cylinder whose base radius is 3 is inscribed in a sphere of radius 5. what is the difference between the volume of the sphere annd the volume of the cylinder?A88B297C354D448A right circular cone whose base radius is 4 is inscribed in a sphere of radius 5. what is the ratio of the volume of the cone to the volume of the sphere?
A0.222:1B0.256:1C0.288:1D0.333:1The volume of a sphere is given by the formula 4V=πr3 , where r is the radius of the sphere.Which of the following gives the radius of the sphere in terms of the volume of the sphere?
A4π3VB3V4πC3√4π3VD3√3V4π
A sphere is placed in an inverted hollow conical vessel of base radius 5cm and vertical height 12cm. If the highest point of the sphere is at the level of the base of the cone, find the radius of the sphere. Show that the volume of the sphere and the conical vessel are as 40: 81.
View SolutionIf a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
View SolutionA square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
View Solution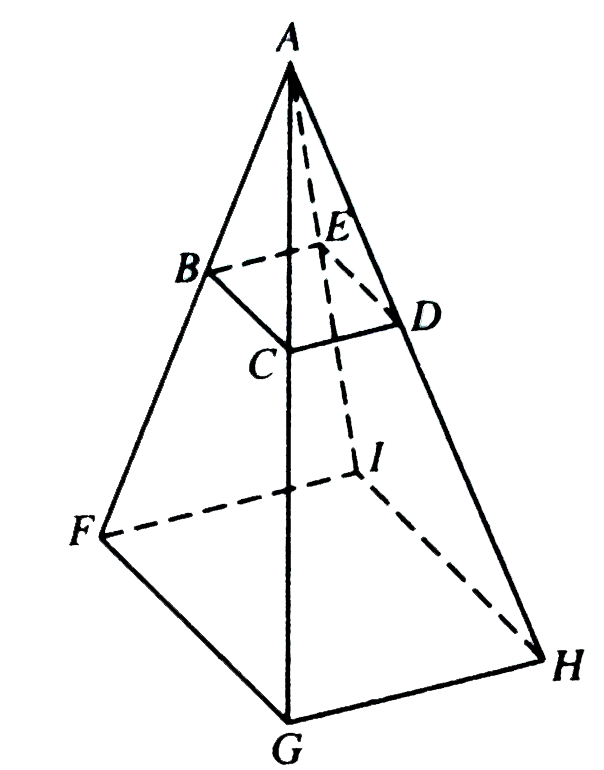
The pyramid in the figure above has square base FGHI , and all triangular faces are congruent. The base BCDE of the small pyramid is also square , and is parallel to FGHI. If the ratio of the area of square BCDE to the area of square FGHI is 1:4 , what is the ratio of the volume of the small pyramid to the volume of the large pyramid ?
View SolutionIf a sphere of radius 3 is inscribed in a cube such that it is tangent to all six faces of the cube, the volume contained outside the sphere and inside the cube is
View Solution

