Suppose ∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0 where f(x) is continuously differentiable function with f'(x)≠0 and satisfies f(0) = 1 and f'(0) = 2 then limx→0f(x)−1x is
1
2
1/2
0
The correct Answer is:B
∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0
⇒ f'(x)f'(x)−f(x).f''(x)=0
⇒ (f(x))2−f(x)f''(x)(f'(x))2=0
⇒ ddx[f(x)f'(x)]=0
⇒ f(x)f'(x)=C (i)
Put x=0,f(0)f'(0)=C⇒C=12
Hence f(x)f'(x)=12
From (i), 2f(x)=f'(x)
∴ f'(x)f(x)=2
∴ ddx(logf(x))=2
∴ log(f(x))=2x+k
Putting x = 0, we get k = 0
⇒ f(x)=e2x
⇒ limx→0e2x−1x=2
Topper's Solved these Questions
- METHODS OF DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:METHODS OF DIFFERENTIATIONExercise:Single Correct Answer Type
Explore 46 Videos
- MATRICESBook:CENGAGE ENGLISHChapter:MATRICESExercise:Single correct Answer
Explore 34 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGE ENGLISHChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Matrix Match Type
Explore 14 Videos
Similar Questions
Suppose ∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0 where f(x) is continuous differentiable function with f'(x)≠0 and satisfies f(0)=1 and f'(0)=2, then f(x)=eλx+k, then λ+k is equal to ..........
View SolutionSuppose ∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0 is continuously differentiable function with f′(x)≠0 and satisfies f(0)=1 and f'(0)=2 then (lim)x→0f(x)−1x is 1/2 b. 1 c. 2 d. 0
View SolutionA differentiable function f(x) satisfies f(0)=0andf(1)=sin1, then (where f' represents derivative of f)
View SolutionFor a differentiable function f(x), if f'(2)=2andf'(3)=1, then the value of limx→0f(x2+x+2)−f(2)f(x2−x+3)−f(3) is equal to
View SolutionIf f(x) is a differentiable function satisfying |f'(x)|≤4∀x∈[0,4] and f(0)=0, then
View SolutionLet f be differentiable function such that
f'(x)=7−34f(x)x,(x>0)andf(1)≠4 Then limx→0+xf(1x)
View SolutionEvaluate limx→0f(x), where
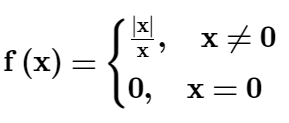
View SolutionA function f satisfies the condition f(x)=f'(x)+f''(x)+f'''(x)+…, where f(x) is a differentiable function indefinitely and dash denotes the order the derivative. If f(0) = 1, then f(x) is
View SolutionLet f''(x) be continuous at x = 0 and f"(0) = 4 then value of limx→02f(x)−3f(2x)+f(4x)x2
View SolutionLet f(x)={xnsin 1xx≠00x=0 Then f(x) is continuous but not differentiable at x=0. If
View Solution

