Match the differential equation in List I with its solution in List II and then choose the correct code.


Text Solution
The correct Answer is:2
a) y=kx+k2
⇒dydx=k
Put the value of k
⇒y=xdydx+(dydx)2
b) y=ae2x+be3x
⇒e−5x/2y=ae−x/2+bex/2
Differentiating w.r.t. x,
−52e−5x/2y+e−5x/2dydx=12[−ae−x/2+bex/2]
Again differentiating w.r.t. x,
254e−5x2,y−52e−5x2dydx
−52e−5x2dydx+e−5x2d2ydx2=14[aex2+bex2]
⇒254e−5x/2y−5e−5x/2d2ydx2=14e−5x/2y
d2ydx2−5dydx+254y−14y=0
d2ydx2−5dydx+6y=0
c) y2=4a(x+a)
⇒yy′=2a
Substitute the value of a in the equation of the curve.
d) xy=aex+be−x+x2
⇒xdydx+y=aex+be−x+2
⇒d2ydx2+2dydx−xy+x2=2
|
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBook:CENGAGE ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:Comprehension Type
Explore 2 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
- DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:DIFFERENTIATIONExercise:Archives
Explore 14 Videos
Similar Questions
Knowledge Check
Match List I with List II and choose the correct code
 AA B C D1 2 3 4BA B C D3 4 1 2CA B C D1 2 3 4DA B C D2 3 1 4
AA B C D1 2 3 4BA B C D3 4 1 2CA B C D1 2 3 4DA B C D2 3 1 4Match the relation for derivatives given in List II with the relation given in List I and then choose the correct code.
 AabcdqpsrBabcdspqrCabcdrqspDabcdqprs
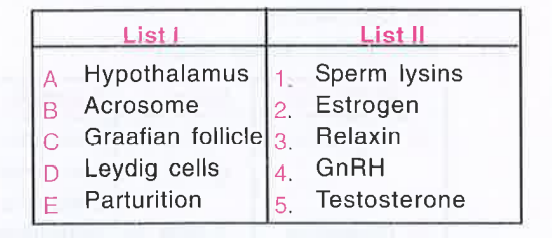
AabcdqpsrBabcdspqrCabcdrqspDabcdqprsMatch list I with list II and choose the correct option:
 AA-4, B-3, C-1, D-2BA-3, B-4, C-1, D-2CA-3, B-1, C-4, D-2DA-2, B-3, C-4, D-1
AA-4, B-3, C-1, D-2BA-3, B-4, C-1, D-2CA-3, B-1, C-4, D-2DA-2, B-3, C-4, D-1
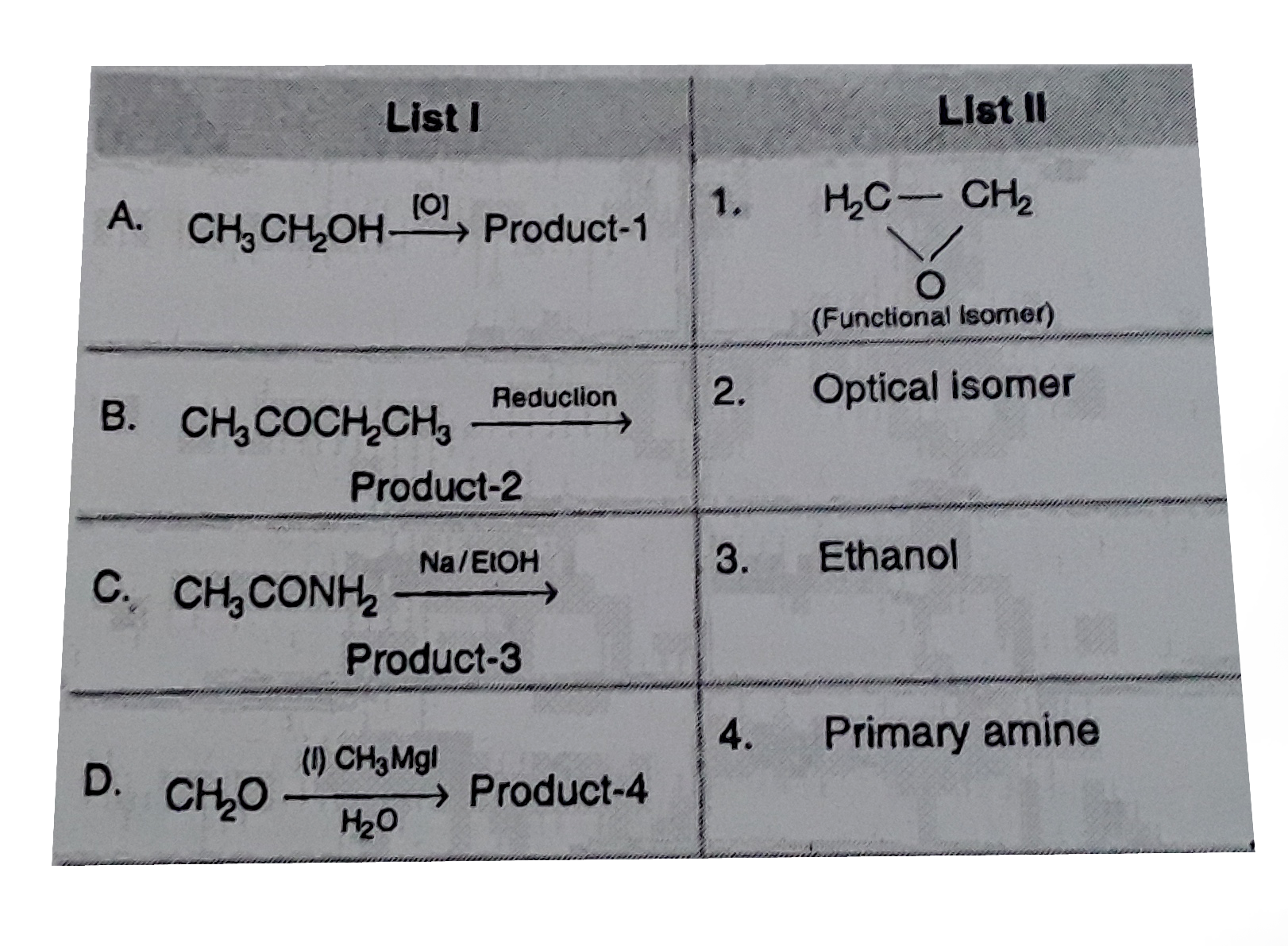
Match list I with list II and choose the correct answer
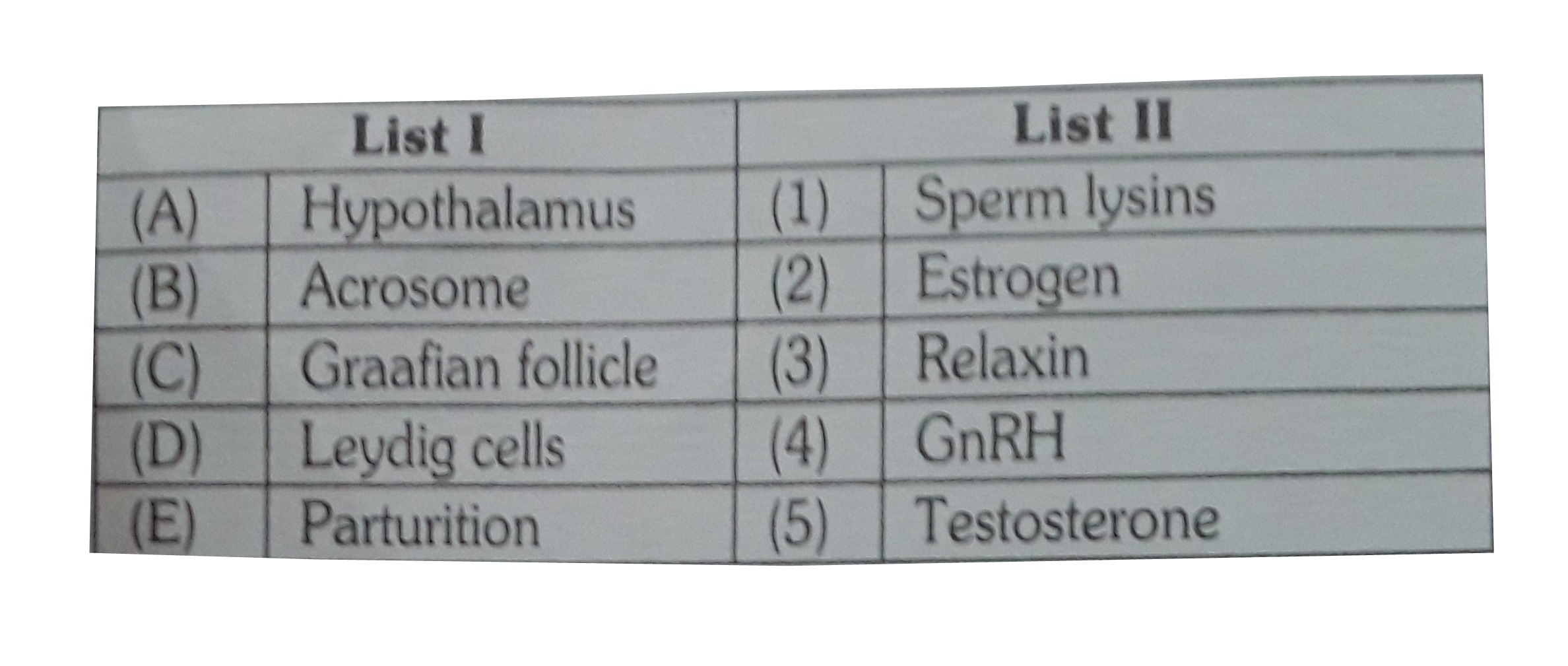
View SolutionMatch the hormone of in the List I with function in the List-II and choose the correct option .
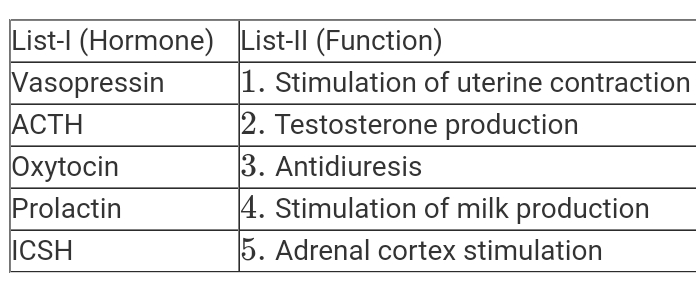
View SolutionMatch list I with II and choose the correct answer

View SolutionMatch List-I with List-II and choose the correct response :
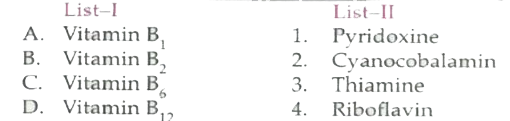
View SolutionMatch the hormone of in the List I with function in the List-II and choose the correct option .

View Solution