Let S=S1∩S2∩S3, where s1={z∈C|z∣<4},S2={z∈C:ln[z−1+√3i1−√31]>0}and
S3={z∈C:Rez>0} Area of S=
10π3
20π3
16π3
32π3
The correct Answer is:B
To find the area of the set S=S1∩S2∩S3, we will analyze each set and then determine the area of their intersection.
Step 1: Define the sets
1. Set S1:
S1={z∈C:|z|<4}
This represents the interior of a circle with radius 4 centered at the origin.
2. Set S2:
S2={z∈C:ln(z−1+√3i1−√3i)>0}
The logarithm is positive when the argument is in the upper half-plane. Thus, we need to find when:
z−1+√3i1−√3i is in the upper half-plane.
This can be simplified to find the line equation.
3. Set S3:
S3={z∈C:Re(z)>0}
This represents the right half-plane.
Step 2: Analyze S2
To analyze S2:
- Let z=x+yi, where x and y are real numbers.
- We need to find when:
Im((x−1)+(y+√3)i1−√3i)>0
- The denominator can be simplified:
1−√3i=1+√3i⟹multiply by its conjugate.
- This leads to the line equation:
√3x+y>0⟹y>−√3x
Step 3: Combine the sets
Now we have:
- S1: Circle of radius 4.
- S2: Area above the line y=−√3x.
- S3: Right half-plane.
Step 4: Find the intersection
The intersection S=S1∩S2∩S3 will be the area of the circle in the right half-plane above the line y=−√3x.
Step 5: Calculate the area
1. Area of the circle:
Area of S1=πr2=π(42)=16π
2. Area of the sector:
- The angle corresponding to the line y=−√3x is 60∘ (since tan(60∘)=√3).
- The area of the sector in the right half-plane:
Area of sector=60360⋅16π=16⋅16π=8π3
3. Area of the triangle:
- The triangle formed by the origin and the intersection points with the circle and the line.
- The vertices are at (0,0), (4,0), and the intersection point on the line.
- The area of the triangle can be calculated using base and height.
Final Area Calculation
The total area of S:
Area of S=Area of sector+Area of triangle
Using the calculated values:
Area=16π⋅16+Area of triangle
Conclusion
The area of the intersection S is:
Area=20π3
S1={z∈C:|z|<4}
This represents the interior of a circle with radius 4 centered at the origin.
S2={z∈C:ln(z−1+√3i1−√3i)>0}
The logarithm is positive when the argument is in the upper half-plane. Thus, we need to find when:
z−1+√3i1−√3i is in the upper half-plane.
This can be simplified to find the line equation.
S3={z∈C:Re(z)>0}
This represents the right half-plane.
- Let z=x+yi, where x and y are real numbers.
- We need to find when:
Im((x−1)+(y+√3)i1−√3i)>0
- The denominator can be simplified:
1−√3i=1+√3i⟹multiply by its conjugate.
- This leads to the line equation:
√3x+y>0⟹y>−√3x
- S1: Circle of radius 4.
- S2: Area above the line y=−√3x.
- S3: Right half-plane.
Area of S1=πr2=π(42)=16π
- The angle corresponding to the line y=−√3x is 60∘ (since tan(60∘)=√3).
- The area of the sector in the right half-plane:
Area of sector=60360⋅16π=16⋅16π=8π3
- The triangle formed by the origin and the intersection points with the circle and the line.
- The vertices are at (0,0), (4,0), and the intersection point on the line.
- The area of the triangle can be calculated using base and height.
Area of S=Area of sector+Area of triangle
Using the calculated values:
Area=16π⋅16+Area of triangle
Area=20π3
Topper's Solved these Questions
- COMPLEX NUMBERSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERSExercise:NUMERICAL VALUE TYPES
Explore 33 Videos
- COMPLEX NUMBERSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERSExercise:ARCHIVES (SINGLE CORRECT ANSWER TYPE )
Explore 11 Videos
- COMPLEX NUMBERSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERSExercise:MULTIPLE CORRECT ANSWERS TYPE
Explore 49 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
- CONIC SECTIONSBook:CENGAGE ENGLISHChapter:CONIC SECTIONSExercise:All Questions
Explore 101 Videos
Similar Questions
Let S=S1∩S2∩S3, where s1={z∈C|z∣<4},S2={z∈C:ln[z−1+√3i1−√31]>0}and
S3={z∈C:Rez>0} Area of S=
View SolutionLet S=S1∩S2∩S3, where S1={zinC:|z|<4},
S2={z inC:Im[z−1+√3i1−√3i]>0}andS3={zinC:Rez>0}
minz∈S|1−3i−z|=
View SolutionLet w = (√3+ι2) and P={wn:n=1,2,3,.....}, Further H1={z∈C:Re(z)>12}andH2={z∈c:Re(z)<−12} Where C is set of all complex numbers. If z1∈P∩H1,z2∈P∩H2 and O represent the origin, then ∠Z1OZ2 =
View SolutionLet 0≠a,0≠b∈R. Suppose
S={z∈C,z=1a+ibtt∈R,t≠0}, where i=√−1. If z=x+iy and z∈S, then (x,y) lies on
View SolutionThe equation of a circle S1 is x2+y2=1. The orthogonal tangents to S1 meet at another circle S2 and the orthogonal tangents to S2 meet at the third circle S3. Then (A) radius of S2andS3 are in ratio 1:√2 (B) radius of S2andS1 are in ratio 1:2 (C) the circles S1,S2andS3 are concentric (D) none of these
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. The co-ordinates of P1 are :
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
The ratio area(ΔP1P2P3)area(ΔC1C2C3) is equal to
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. P2andP3 are image of each other with respect to line :
View SolutionConsider the region S of complex numbers a such that ∣∣z2−az+1∣∣=1, where |z|=1 . Then area of S in the Argand plane is
View SolutionIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
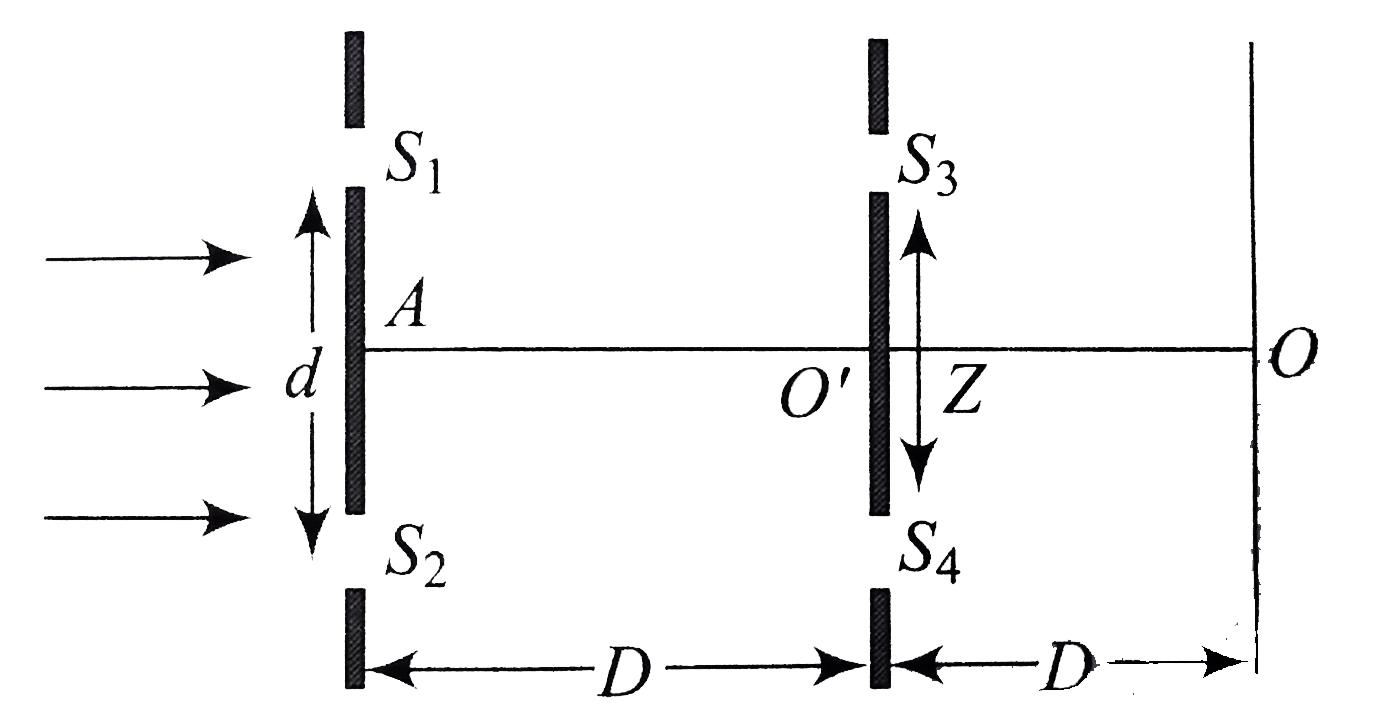
The minimum value of Z for which the intensity at O is zero is
View Solution