Let z be a complex number satisfying equation zp−z−q=0, where p,q∈N,then (A) if p=q , then number of solutions of equation will be infinite. (B) if p=q , then number of solutions of equation will be finite. (C) if p≠q , then number of solutions of equation will be p+q+1. (D) if p≠q , then number of solutions of equation will be p+q.

A

if p=q, then number of solution of equation will infinte.

B

if p=q, then number of solutions of equaiton will finite

C

if p≠q, then number of solutions of equaiton will p+q+1.

D

if p≠q, then number of solutions of equaiton will be p+q

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A, B

If q=p, then equation becomes zp=z−q and it has infinte
number of solutions because any z ∈ R will satisfly it. p≠q,
let p>q, then zp=z−q

Updated on:21/07/2023
|
Class 12MATHSCOMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The following diagram represents the solution of two sets P and Q on the number line:
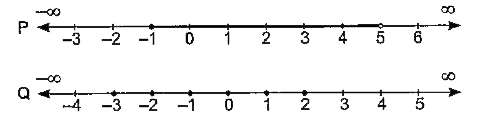
    ocr_image
    The solution set of Q in set builder form is:

    A{x:−3<x<2,x∈R}
    B{x:−3≤x≤2,x∈I}
    C{x:−3<x≤2,x∈N}
    D{x:−3≤x<2,x∈W}

  • The following diagram represents the solution of two sets P and Q on the number line:
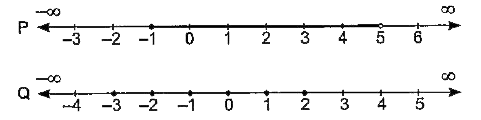
    ocr_image
    The solution set of Q in roaster form is:

    A{−2,−1,0,1}
    B{1, 2}
    C{−3,−2,−1,0,1,2}
    D{0,1,2}

  • The following diagram represents the solution of two sets P and Q on the number line:
    ocr_image
    The solution set of P in set-builder form is

    A{x:−1<x≤5,x∈R}
    B{x:−1≤x<5,x∈R}
    C{x:−1≤x≤5,x∈R}
    D{x:−1<x<5,x∈R}