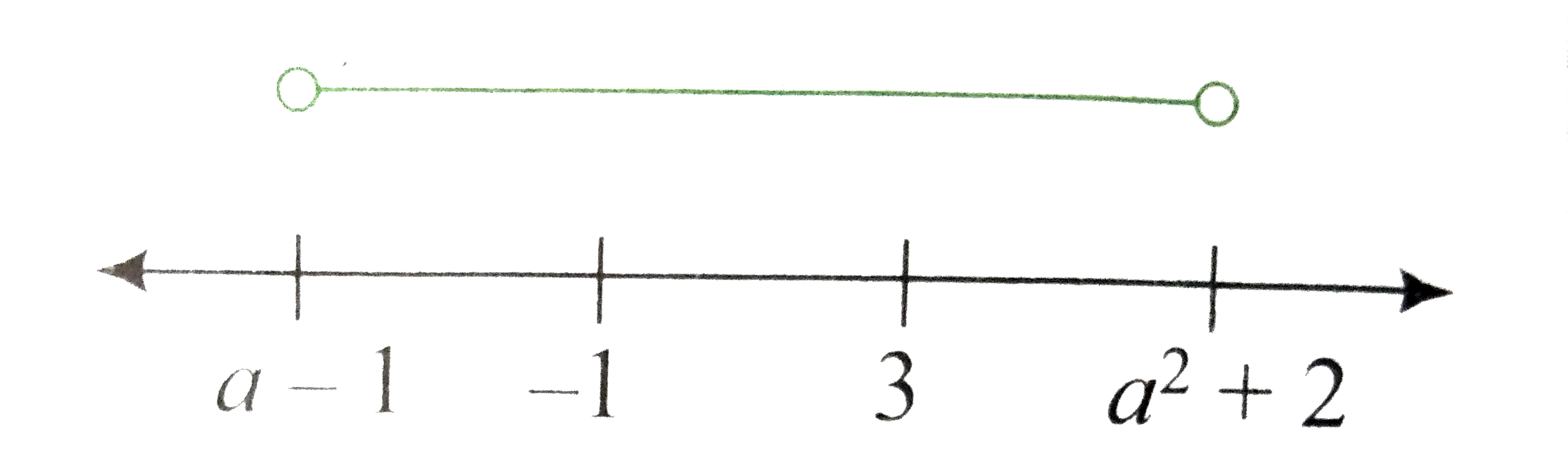
Find the set of all possible real value of a such that the inequality (x−(a−1))(x−(a2+2))<0 holds for all x∈(−1,3).
(0,1)
(∞,−2]
(−∞,−1)
(1,∞)
The correct Answer is:2
We have,
a−1≤−1
and a2+2≥3
a≤0anda2≥1
Hence, a ≤−1
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Linked Comprechension Type
37 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.13
9 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
The set of all possible real values of a such that the inequality (x−(a−1))(x−(a2−1))<0 holds for all x∈(−1,3) is (0,1) b. (∞,−1] c. (−∞,−1) d. (1,∞)
View SolutionFind the set of all real values of x satisfying the inequality sec−1x>tan−1x.
View SolutionFind the possible values of 'a' such that the inequality 3−x2>|x−a| has atleast one negative solution
View SolutionThe set of real values of x satisfying the inequality ∣∣x2+x−6∣∣<6, is
View SolutionLet set of all possible values of λ such that f(x)=e2x−(λ+1)ex+2x is monotonically increasing for ∀x∈R is (−∞,k]. Find the value of k.
View SolutionFind all possible values of
√|x|−2
.
View SolutionFind the sum of all real values of X satisfying the equation (x2−5x+5)x2+4x−60=1 .
View SolutionFind all possible values of x2+1x2−2 .
View SolutionFind all possible values of x2+1x2−2 .
View SolutionThe set of all values of x satisfying the inequations (x−1)3(x+1)<0 is
View Solution
