Three straight lines mutually perpendicular to each other meet in a point P and one of them intersects the x-axis and another intersects the y-axis, while the third line passes through a fixed point(0,0,c) on the z-axis. Then the locus of P is
x2+y2+z2−2cx=0
x2+y2+z2−2cy=0
x2+y2+z2−2cz=0
x2+y2+z2−2c(x+y+z)=0
The correct Answer is:C
To solve the problem, we need to find the locus of the point P where three mutually perpendicular lines intersect. One line intersects the x-axis, another intersects the y-axis, and the third line passes through a fixed point on the z-axis, specifically (0, 0, c).
1. Define the Points of Intersection:
- Let the point where line L1 intersects the x-axis be A(a, 0, 0).
- Let the point where line L2 intersects the y-axis be B(0, b, 0).
- The line L3 intersects the z-axis at the fixed point C(0, 0, c).
2. Coordinates of Point P:
- Let P be the point of intersection of the three lines, which can be represented as P(x, y, z).
3. Direction Ratios of the Lines:
- The direction ratios (DRs) for line L1 can be represented as (x - a, y, z).
- The direction ratios for line L2 can be represented as (x, y - b, z).
- The direction ratios for line L3 can be represented as (x, y, z - c).
4. Using the Condition of Perpendicularity:
- Since the lines are mutually perpendicular, the dot product of the direction ratios of any two lines must equal zero.
5. Equation from L1 and L2:
- The dot product of L1 and L2:
(x−a)(x)+(y)(y−b)+(z)(z)=0
- Expanding this gives:
x2−ax+y2−by+z2=0(Equation 1)
6. Equation from L2 and L3:
- The dot product of L2 and L3:
(x)(x)+(y−b)(y)+(z)(z−c)=0
- Expanding this gives:
x2+y2−by+z2−cz=0(Equation 2)
7. Equation from L1 and L3:
- The dot product of L1 and L3:
(x−a)(x)+(y)(y)+(z)(z−c)=0
- Expanding this gives:
x2−ax+y2+z2−cz=0(Equation 3)
8. Combining Equations:
- By adding Equation 2 and Equation 3, we can eliminate some terms:
(x2+y2+z2)−(ax+by+cz)=0
- Rearranging gives:
x2+y2+z2−2cz=0
9. Final Locus Equation:
- Replacing x, y, z with their respective coordinates gives us:
x2+y2+z2−2cz=0
- This represents the locus of point P.
Conclusion:
The locus of point P is given by the equation:
x2+y2+z2−2cz=0
- Let the point where line L1 intersects the x-axis be A(a, 0, 0).
- Let the point where line L2 intersects the y-axis be B(0, b, 0).
- The line L3 intersects the z-axis at the fixed point C(0, 0, c).
- Let P be the point of intersection of the three lines, which can be represented as P(x, y, z).
- The direction ratios (DRs) for line L1 can be represented as (x - a, y, z).
- The direction ratios for line L2 can be represented as (x, y - b, z).
- The direction ratios for line L3 can be represented as (x, y, z - c).
- Since the lines are mutually perpendicular, the dot product of the direction ratios of any two lines must equal zero.
- The dot product of L1 and L2:
(x−a)(x)+(y)(y−b)+(z)(z)=0
- Expanding this gives:
x2−ax+y2−by+z2=0(Equation 1)
- The dot product of L2 and L3:
(x)(x)+(y−b)(y)+(z)(z−c)=0
- Expanding this gives:
x2+y2−by+z2−cz=0(Equation 2)
- The dot product of L1 and L3:
(x−a)(x)+(y)(y)+(z)(z−c)=0
- Expanding this gives:
x2−ax+y2+z2−cz=0(Equation 3)
- By adding Equation 2 and Equation 3, we can eliminate some terms:
(x2+y2+z2)−(ax+by+cz)=0
- Rearranging gives:
x2+y2+z2−2cz=0
- Replacing x, y, z with their respective coordinates gives us:
x2+y2+z2−2cz=0
- This represents the locus of point P.
The locus of point P is given by the equation:
x2+y2+z2−2cz=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
The plane 2x+3y-4z=5 intersects the x-axis at (a,0,0), the y-axis at (0,b,0), and the z-axis at (0,0,c). The value of a+b+c is
A1B3512C5D6512Of a line passes through the points (5, 3) and (8, -1), at what point will this line intersect the y - axis ?
A(0,8.33)B(0,8.67)C(0,9.00)D(0,9.67)
Three mutually perpendicular lines are drawn from the point (1,2,−1). If one of the lines is perpendicular to the x-axis and the direction ratios of the second line are (1,2,-1) then which are the possible equation(s) of the third line
View SolutionThe equation of straight line passing through the point (a,b,c) and parallel to Z-axis, is:
View SolutionA line has slope of 16 and intersects the x-axis at (−24,0). At which point does this line intersect the y-axis?
View SolutionTangent to a curve intercepts the y-axis at a point P .A line perpendicular to this tangent through P passes through another point (1,0). The differential equation of the curve is
View SolutionThe line through P(5, 3) intersects y-axis at Q.
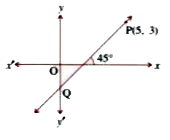
Write the slope of the line.
View SolutionThe straight line through the point of intersection of ax+by+c=0 and a'x+b'y+c'=0 are parallel to the y-axis has the equation
View Solution
