e|sinx|+e−|sinx|+4a=0 will have exactly four different solutions in [0,2π] if. a∈R (b) a∈[−34,−14] a∈[−1−e24e,∞] (d) none of these
a∈R
a∈[−e4,−14]
a∈[−1−e24e,∞]
none of these
The correct Answer is:D
To solve the equation e|sinx|+e−|sinx|+4a=0 and determine the conditions on a for which it has exactly four different solutions in the interval (0,2π), we can follow these steps:
Step 1: Rewrite the Equation
We start with the equation:
e|sinx|+e−|sinx|+4a=0
This can be rewritten as:
e|sinx|+1e|sinx|+4a=0
Step 2: Substitute t
Let t=e|sinx|. Since |sinx| varies between 0 and 1, t will vary between e0=1 and e1=e.
Step 3: Transform the Equation
Substituting t into the equation gives:
t+1t+4a=0
This simplifies to:
t+1t=−4a
Step 4: Analyze the Function
Define the function:
f(t)=t+1t
We need to analyze this function for t in the interval (1,e).
Step 5: Find the Range of f(t)
To find the minimum and maximum values of f(t):
- The derivative f′(t)=1−1t2.
- Setting f′(t)=0 gives t2=1 or t=1 (since t is positive).
- Evaluate f(t) at the endpoints:
- f(1)=1+1=2
- f(e)=e+1e
Calculating f(e):
f(e)=e+1e≈2.718+0.368=3.086
Thus, the range of f(t) for t∈(1,e) is:
(2,e+1e)
Step 6: Set Up the Inequality
For the equation −4a to fall within the range of f(t):
−4a∈(2,e+1e)
This leads to:
2≤−4a≤e+1e
Step 7: Solve for a
From −4a≥2:
a≤−12
From −4a≤e+1e:
a≥−e+1e4
Step 8: Final Range for a
Thus, we have:
−e+1e4≤a≤−12
Step 9: Check the Options
Now we check the provided options:
- (a) a∈R - Incorrect.
- (b) a∈(−34,−14) - Incorrect.
- (c) a∈(−1+e24e,∞) - Incorrect.
- (d) None of these - Correct.
Conclusion
The correct answer is:
(d) none of these.
We start with the equation:
e|sinx|+e−|sinx|+4a=0
This can be rewritten as:
e|sinx|+1e|sinx|+4a=0
Let t=e|sinx|. Since |sinx| varies between 0 and 1, t will vary between e0=1 and e1=e.
Substituting t into the equation gives:
t+1t+4a=0
This simplifies to:
t+1t=−4a
Define the function:
f(t)=t+1t
We need to analyze this function for t in the interval (1,e).
To find the minimum and maximum values of f(t):
- The derivative f′(t)=1−1t2.
- Setting f′(t)=0 gives t2=1 or t=1 (since t is positive).
- Evaluate f(t) at the endpoints:
- f(1)=1+1=2
- f(e)=e+1e
f(e)=e+1e≈2.718+0.368=3.086
Thus, the range of f(t) for t∈(1,e) is:
(2,e+1e)
For the equation −4a to fall within the range of f(t):
−4a∈(2,e+1e)
This leads to:
2≤−4a≤e+1e
From −4a≥2:
a≤−12
From −4a≤e+1e:
a≥−e+1e4
Thus, we have:
−e+1e4≤a≤−12
Now we check the provided options:
- (a) a∈R - Incorrect.
- (b) a∈(−34,−14) - Incorrect.
- (c) a∈(−1+e24e,∞) - Incorrect.
- (d) None of these - Correct.
The correct answer is:
(d) none of these.
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercises (Multiple correct type)
31 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercises (Linked comprehension type)
20 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Concept Application Exercise 4.9
6 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE
1 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
e|sinx|+e−|sinx|+4a=0 will have exactly four different solutions in [0,2π] . Find the value of a. (a) a∈R (b) a∈[−34,−14] (c)a∈[−1−e24e,∞] (d) none of these
View SolutionIf sin2x−2sinx−1=0 has exactly four different solutions in x∈[0,nπ] , then value/values of n is/are (n∈N) 5 (b) 3 (c) 4 (d) 6
View SolutionGeneral solution for |sinx|=cosx is (a) 2nπ+π4, n∈I (b) 2nπ±π4,n∈1 (c) nπ+π4, n∈1 (d) none of these
View SolutionIf esinx−e−sinx−4=0 , then x= (a) 0 (b) sin−1{(log)e(2+√5)} (c) 1 (d) none of these
View SolutionIf both the distinct roots of the equation |sinx|2+|sinx|+b=0∈[0,π] are real, then the values of b are [−2,0] (b) (−2,0) [−2,0] (d) noneofthese
View SolutionIf both the distinct roots of the equation |sinx|2+|sinx|+b=0∈[0,π] are real, then the values of b are [−2,0] (b) (−2,0) [−2,0] (d) noneofthese
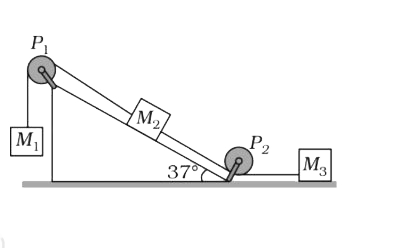
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View SolutionThe number of solution of equation sin−1x+nsin−1(1−x)=mπ2,wheren>0,m≤0, is 3 (b) 1 (c) 2 (d) None of these
View SolutionThe number of solutions of the equation |cosx−sinx|=2cosx∈[0,2π] is (A) 1 (B) 2 (C) 3 (D) 4
View SolutionIf y=cos−1(5cosx−12sinx13),wherex∈(0,π2), then dydx is. (a)1 (b) −1 (c) 0 (d) none of these
View Solution
