Question

A
particle just clears a wall of height b at distance a and strikes the ground
at a distance c from the point of projection. The angle of projection is
(1) $\frac{{\tan }^{-1}b}{ac}$

(2) ${\text{45}}^o$

(3) $\frac{{\tan }^{-1}\left(bc\right)}{a(c-a)}$

(4) $\frac{{\tan }^{-1}\left(bc\right)}{a}$

Options

A. `(3,0) and (0,2)`
B. `(-8//5,2sqrt(161)//15) and (-9//5,8//5)`
C. `(8//5,2sqrt(161)//15 and (0,2)`
D. `(3,0) and (-9//5,8//5)`

Explanation

Given ellipse `(x^(2))/(9)+(y^(2))/(4)=1`
The equation of tangent having slope m is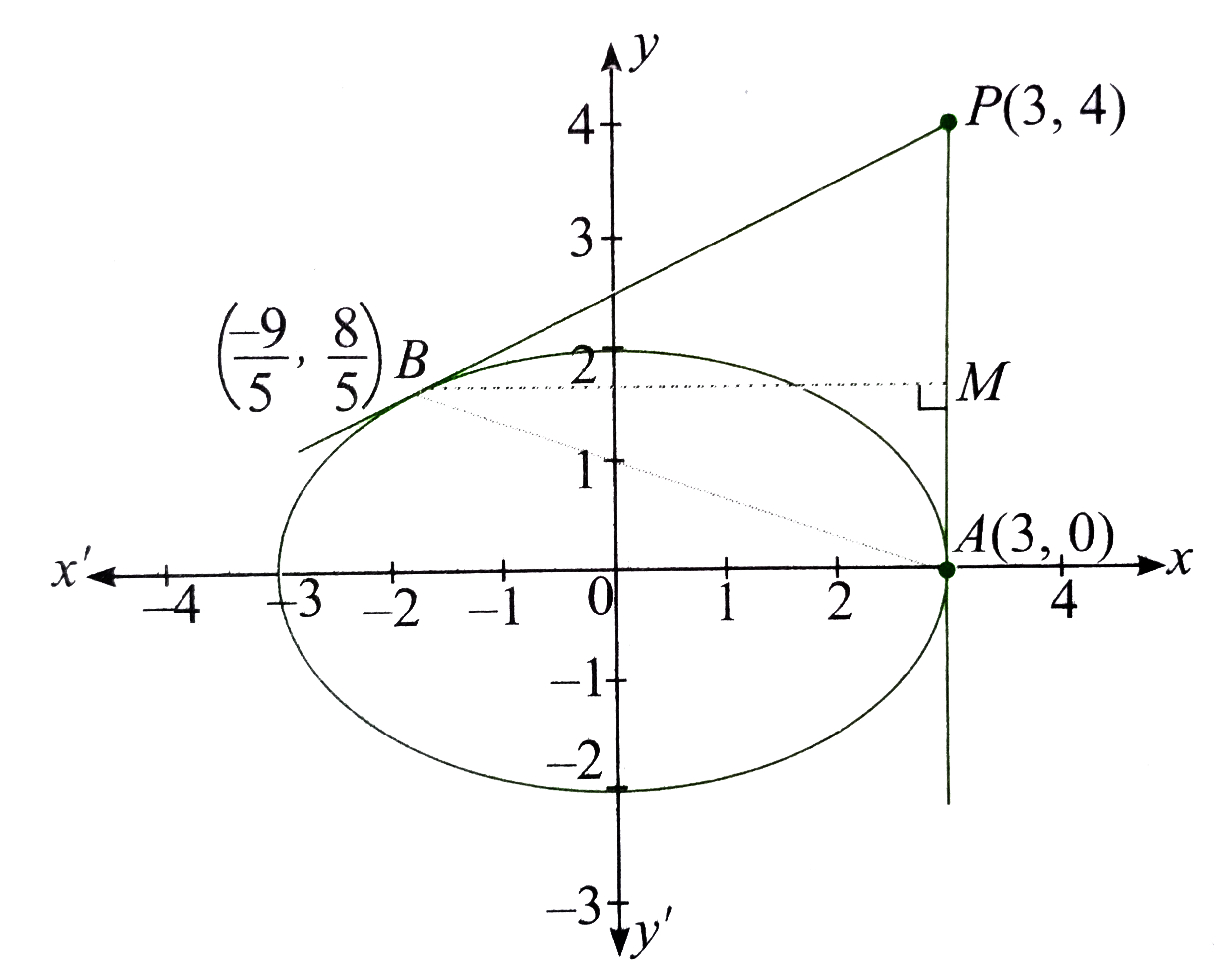
`y=mx+sqrt(9m^(2)+4)`
Sqaring , we have
`16+9m^(2)-24m=9m^(2)+4`
or `m=(12)/(24)=(1)/(2)`
Threrefpre, the equation of tangent is `y-4=-(x-3)pr x-2y+5=0 " "(1)`
Let the point of contact on the curve be `B(alpha,beta)`
Equation of tangent at this point is `(xalpha)/(9)+(ybeta)/(4)-1=0" "(2)`
Comparing equations (1) and (2)
`(alpha//9)/(1)=(beta//4)/(-2)=-(1)/(5)`
or `alpha=-(9)/(5),beta=(8)/(5)" " :. B-=(-(9)/(5),(8)/(5))`
Another slope of tangent is `oo` then the equation of tanents is `x=3` and the coresponding point of cocntact is A(3,0)