The normal at a point P on the ellipse x2+4y2=16 meets the x-axis at Q. If M is the midpoint of the line segment PQ, then the locus of M intersects the latus rectums of the given ellipse at points. ⎛⎜ ⎜⎝±(3√5)2±27⎞⎟ ⎟⎠ (b) ⎛⎜ ⎜⎝±(3√5)2±√197⎞⎟ ⎟⎠ (±2√3,±17) (d) (±2√3±4√37)
(±3√5/2,±2/7)
(±3√5/2,±√19/7)
±2√3,±17)
(±2√3,±4√3/7)
Given ellipse is x216+y24=1. Normal at P(4cosϕ,2sinϕ),
given by 4xsecϕ−2ycosecϕ=12
It meets x-axist at
Let M≡(α,β)
be the point of PQ.
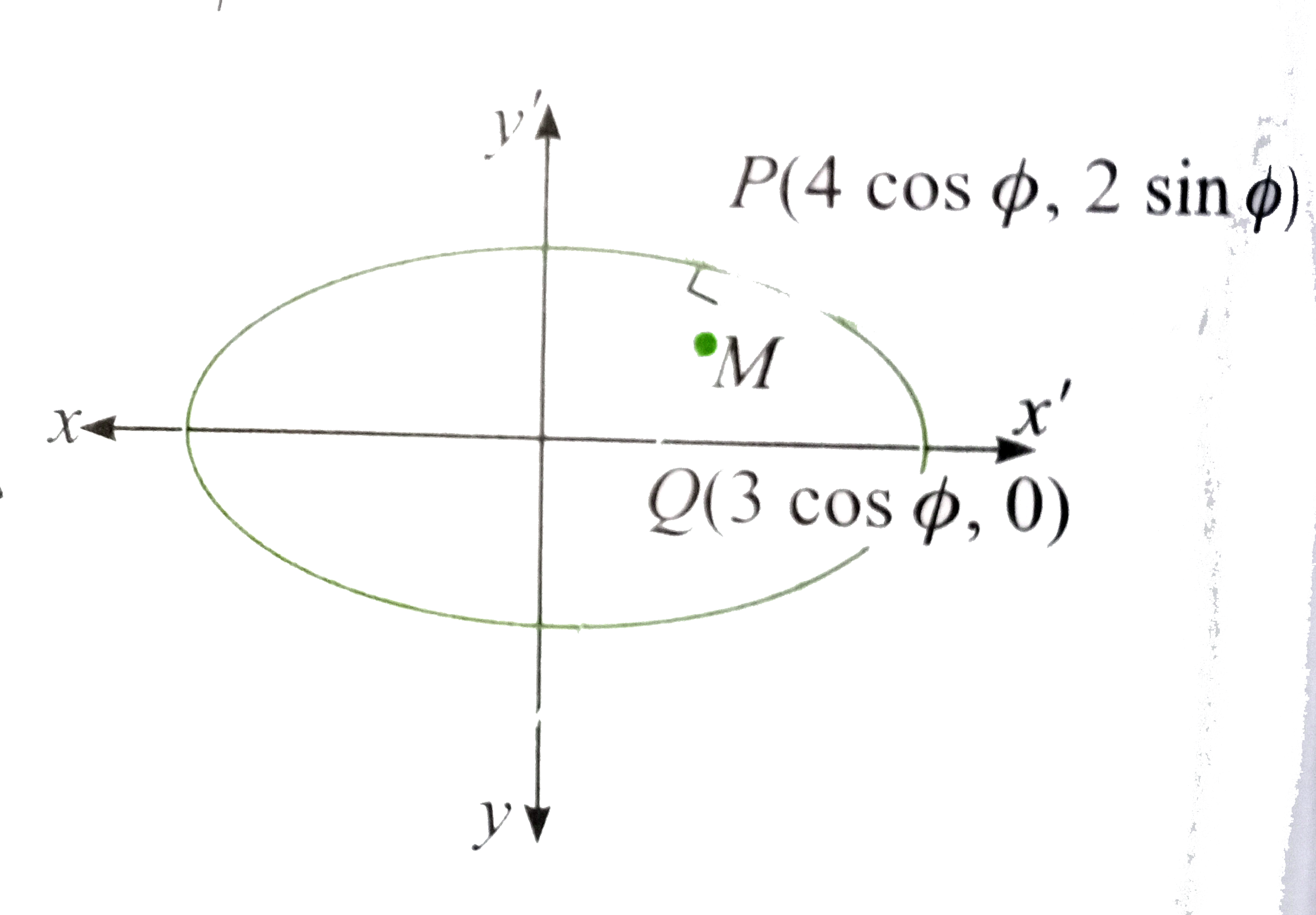
∴α=3cosϕ+4cosϕ2
=72cosϕ
or cosϕ=27α
Using cos2ϕ+sin2ϕ=1, we have
449α2+β2=1
or 449x2+y2=1
Now, the rectum lines of given ellipse are x=±2√3
Solving (1) and (2), we have
4849+y2=1
ory=±17
The points of intersection are (±2√3,±1/7)
Similar Questions
The normal at a point P on the ellipse x2+4y2=16 meets the x-axis at Q. If M is the midpoint of the line segment PQ, then the locus of M intersects the latus rectums of the given ellipse at points. (a)⎛⎜ ⎜⎝±(3√5)2±27⎞⎟ ⎟⎠ (b) ⎛⎜ ⎜⎝±(3√5)2±√197⎞⎟ ⎟⎠ (c)(±2√3,±17) (d) (±2√3±4√37)
View Solution(√7+2√3)(√7−2√3)
View Solution
Knowledge Check
The length of latus rectum of the ellipse 3x2+y2=12 is (i) 4 (ii) 3 (iii) 8 (iv) 4√3
A4B3C8D4√3
The eccentricity of the ellipse 4x2+9y2=36 is a.12√3 b. 1√3 c. √53 d. √56
View SolutionThe eccentricity of the ellipse 4x2+9y2=36 is
a.12√3
b. 1√3
c. √53
d. √56
View SolutionFind the 5th term of the progression 1,(√2−1)2√3, (3−2√212), (5√2−724√3), ..
View SolutionFactorise: (i) 4√3x2+5x−2√3
(ii) 7√2x2−10x−4√2
View SolutionThe latus rectum of the conic 3x2+4y2−6x+8y−5=0 is a.3 b. √32 c. 2√3 d. none of these
View SolutionSimplify: (i)7+3 √53+ √5−7−3 √53− √5 (ii)12+√3 +2√5− √3+12− √5
View SolutionSimplify each of the following by rationalising the denominator: 7+3√57−3√5 (ii) 2 √3− √52√2+ 3√3
View Solution
