The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latus rectum to the ellipse x29+y25=1 is (a) 274 (b) 18 (c) 272 (d) 27
27/4
18
27/2
27
The correct Answer is:D
The given ellipe is
x29+y25=1
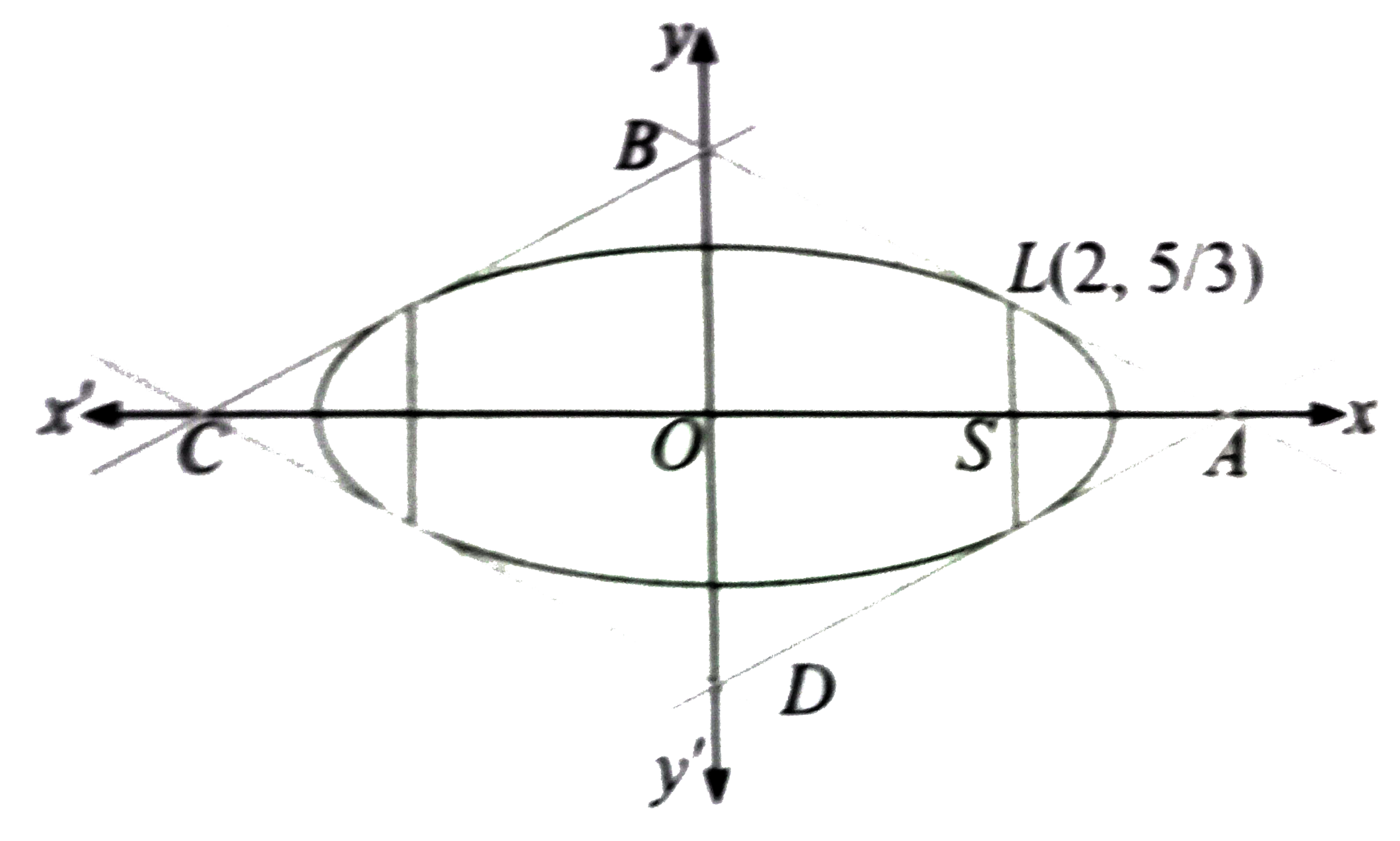
Then a2=9,b2=5. Therefore,
e=√1−59=23 ∴ae=2
Hence, the endpoint of latus rectum in the first quadrant is L(ae,b2/a)≡L(2,5/3)
The equation of tangent at L is 2x9+y3=1
the tangents meets the x-axis at A(9/2,0) and the y-axis at B(0,3). Therefore,
Area of ΔOAPB=12×92×3=274
∴ Area of quadrilateral =4×274=27
Similar Questions
The area (in sq. units) of the triangle formed by the latus rectum and the tangents at the end points of the latus rectum of x216−y29=1 is equal to
View SolutionThe area of the quadrillateral formed by the tangents and normals at the extremities of the latus rectum of the parabola y2−4y+4+12x=0 is
View SolutionFind the area of the triangle formed by the vertex and the ends of the latus rectum of the parabola
x2=−36y.
View SolutionThe length of the latus rectum of the ellipse 2x2+3y2−4x−6y−13=0 is
View SolutionThe area (in sq. units) bounded by the parabola y=x2−1, the tangent at the point (2,3) to it and the y-axis is
View SolutionFind the coordinate of the foci, vertice eccentricity and the length of the latus rectum of the hyperbola
y29−x227=1
View SolutionIntegral part of the area of figure bounded by the tangents at the end of latus rectum of ellipse x29+y24=1 and directices of hyperbola x29+y272=1is
View SolutionThe point of intersection of the tangents at the ends of the latus rectum of the parabola y2=4x is_____________
View Solutionlf a quadrilateral is formed by four tangents to the ellipse x29+y24=1 then the area of the square is equal to
View SolutionThe area (in sq. units) of the triangle formed by the lines y=2x,y=−2x and the tangent at the point (√5,4) on 4x2−y2=4 is equal to
View Solution
