The ellipse x24y2=4 is inscribed in a rectangle aligned with the coordinates axes, whicj in turn is inscribed in another ellipse that passes through the point (0,0). Then, the equation of the ellipse is
x2+16y2=16
x2+12y2=16
4x2+48y2=16
4x2+64y2=48
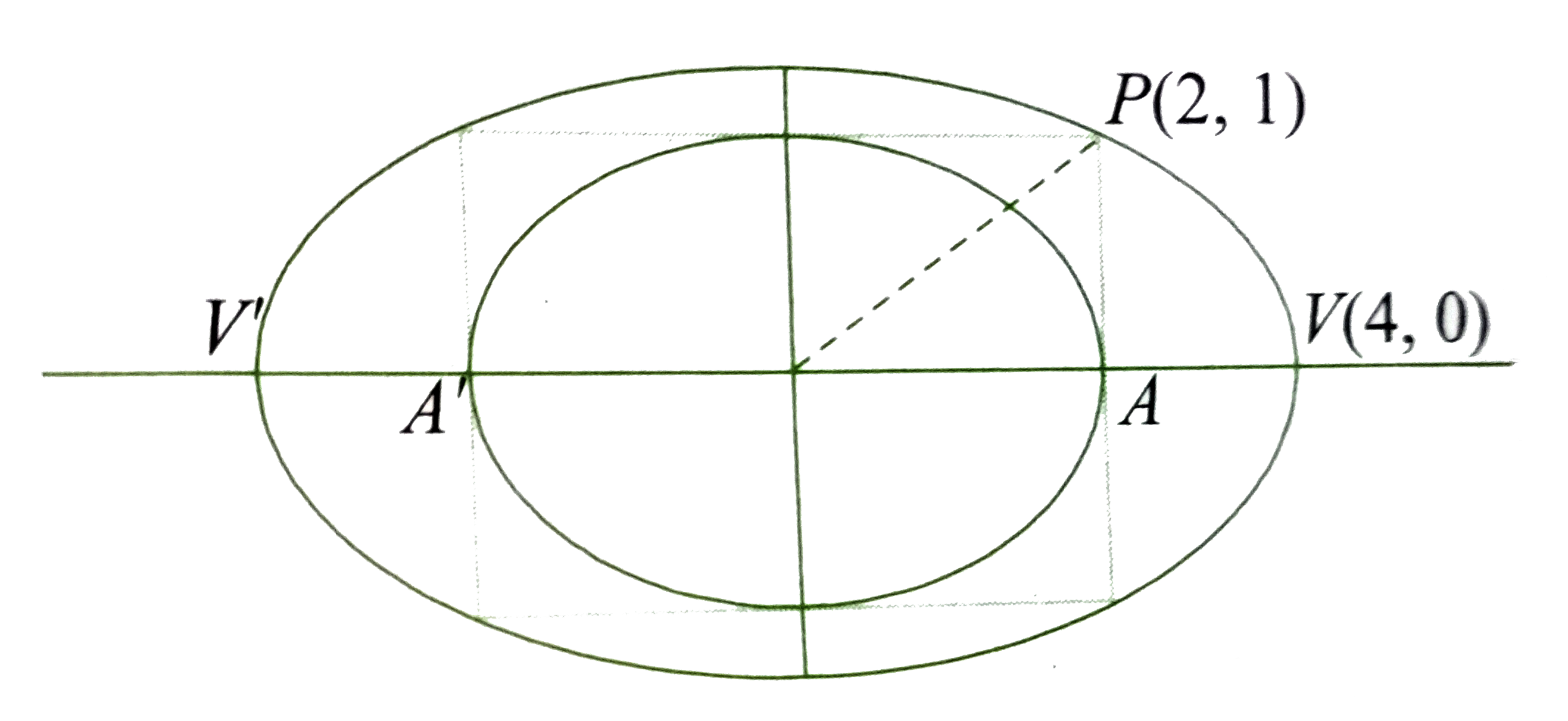
x2+4y2=4⇒x24+y21=1
So, a=2,b=1
Thus P is (2,1)
The required ellipse is x2a2+y2b2=1⇒x242+y2b2=1
The point (2,1) lis on it.So
416+1b2=1⇒1b2=1−14=34⇒b2=43
∴x216+y2(43)=1⇒x216+3y24=1⇒+12y2=16
Similar Questions
The ellipse x2+4y2=4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) x2+16y2=16 (2) x2+12y2=16 (3) 4x2+48y2=48 (4) 4x2+64y2=48
View SolutionThe ellipse x2+4y2=4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) x2+16y2=16 (2) x2+12y2=16 (3) 4x2+48y2=48 (4) 4x2+64y2=48
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionIf the major axis of an ellipse is alongthe y-axis and it passes through the points (0,√3) and (√2,0), then the equation of the elliipse is
View Solutionthe foci of an ellipse are (0±6) and the equation of the directrces are y=±9. the equation of the ellipse is
View SolutionAn ellipse passes through the point (2,3) and its axes along the coordinate axes, 3x+2y−1=0 is a tangent to the ellipse, then the equation of the ellipse is
View SolutionFind the equation of the ellipse passing through the point (3,2), having centre at (0,0) and major axis on y-axis.
View SolutionIf a tangent of slope 2 of the ellipse x2a2+y21=1 passes through the point (−2,0), then the value of a2 is equal to
View SolutionThe eccentricity of an ellipse with centre at the orgin and axes along the coordinate axes , is 1/2 if one of the directrices is x=4, the equation of the ellipse is
View SolutionFind the equation of the ellipse passing through (4, 1) with focus as (±3,0)
View Solution
