Let S and S'' be the fociof the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ whose eccentricity is i.e. P is a variable point on the ellipse. Consider the locus the incenter of $Δ P S S''$
The eccentricity of the locus oc the P is (a) ellipse (b) hyperbola (a) parabola (d) circle

$\sqrt{\frac{2 e}{1 - e}}$

$\sqrt{\frac{2 e}{1 + e}}$

none of these

Video Solution

Text Solution

Verified by Experts

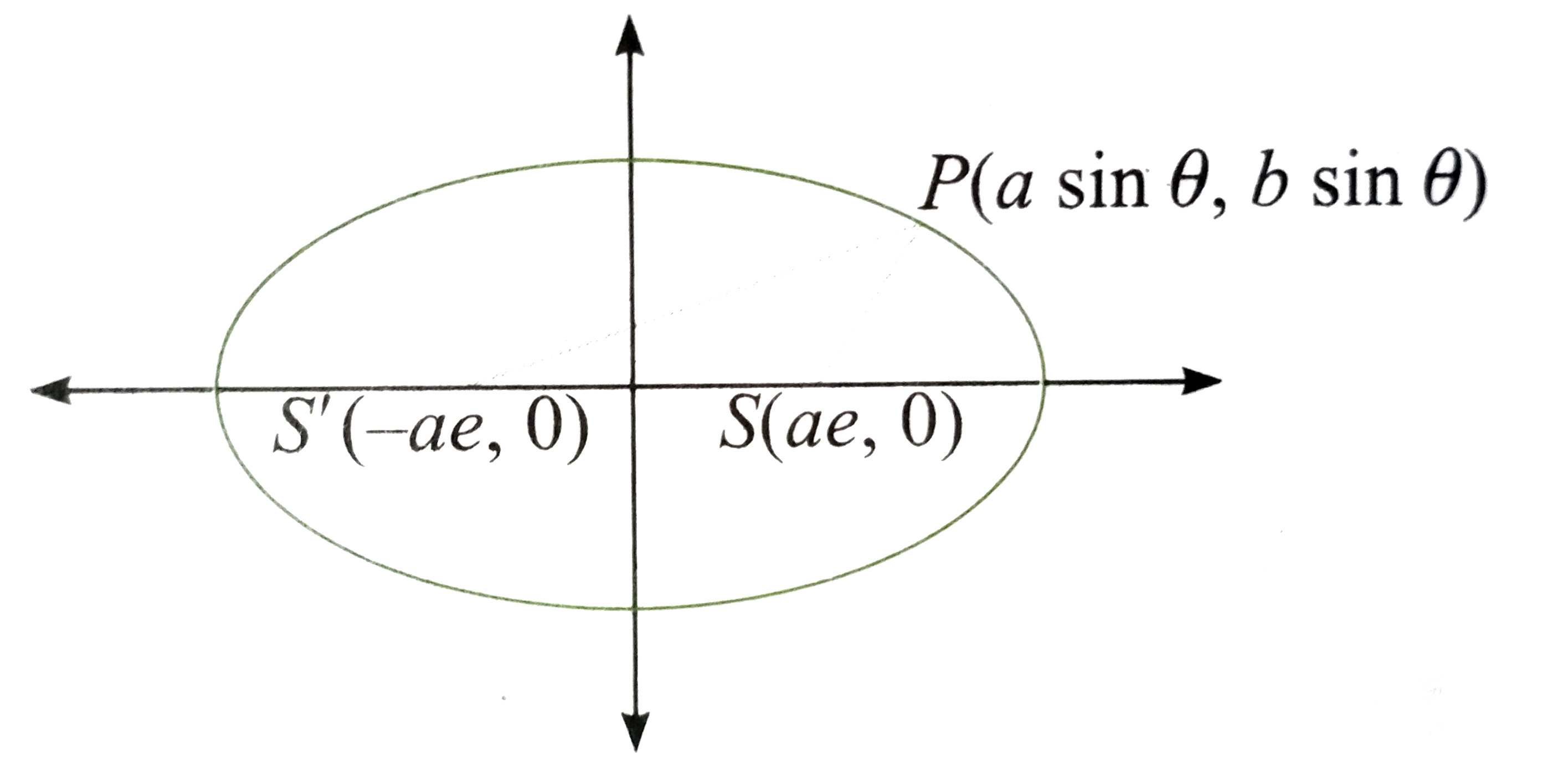
Let the coordinates of P be $(a \cos θ, b \sin θ)$
Here, SP= Focal distance of point $P = a - a e \cos θ$
$S'' P = a + a e \cos θ$
SS''=2ae
If (h,k) are the coordinates of the incenter of $Δ P S S''$ , then
$h = \frac{2 a e (a \cos θ) + a (1 - e \cos θ) (- a e) + a (1 + e \cos θ) a e}{2 a e + a (1 - e \cos θ) + a (1 + e \cos θ)}$
$a s \cos θ (1)$
$and k = \frac{2 a e (a \sin θ) + a (1 - e \cos θ) \times 0 + a (1 + e \cos θ) \times 0}{2 a e + a (1 - e \cos θ) + a (1 + e \cos θ)}$
$= \frac{e b \sin θ}{(e + 1)} (2)$
Eliminating $θ$ from (1) and (2), we get
$\frac{x^{2}}{a^{2} e^{2}} + \frac{y^{2}}{{b e / (e + 1)}^{2}} = 1$
Which clearly represents an ellipse. Let $e_{1}$ be its eccentricity . Then
$\frac{b^{2} e^{2}}{{(e + 1)}^{2}} = a^{2} e^{2} (1 - e_{1}^{2})$
or $e_{1}^{2} = 1 - \frac{b^{2}}{a^{2} {(e + 1)}^{2}}$
$or e_{1}^{2} = 1 - \frac{1 - e^{2}}{(e + 1)} = 1 - \frac{1 - e}{1 + e}$
$or e_{1}^{2} = \frac{2 e}{e + 1}$
$or e_{1} = \sqrt{\frac{2 e}{e + 1}}$
Maximum area of reactangle is
$2 (a e) (\frac{be}{e + 1}) = \frac{2 a b e^{2}}{e + 1}$

Updated on:21/07/2023

In the ellipse $\frac{x^{2}}{6} + \frac{y^{2}}{8} = 1$ , the value of eccentricity is
A $\frac{1}{2}$
B $\frac{2}{3} 2$
C $\frac{1}{3}$
D $\frac{3}{2}$
The eccentricity of the ellipse $\frac{x^{2}}{49} + \frac{y^{2}}{25} = 1$ is
A $\frac{2}{7}$
B $\frac{\sqrt{6}}{7}$
C $\frac{2 \sqrt{6}}{5}$
D $\frac{2 \sqrt{6}}{7}$