Question

Consider an ellipse E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, centered at point 'O' and having AB and CD as its major and minor axes respectively if $S_1$be one of the focus of the ellipse, radius of the incircle of ∆OCS_1 be 1 unit and $O{S}_1=6$units.
Q. The equation of the director circle of (E) is

Options

A. `x^(2)+y^(2)=48.5`
B. `x^(2)+y^(2)=sqrt(97)`
C. `x^(2)+y^(2)=97`
D. `x^(2)+y^(2)=sqrt(48.5)`

Explanation

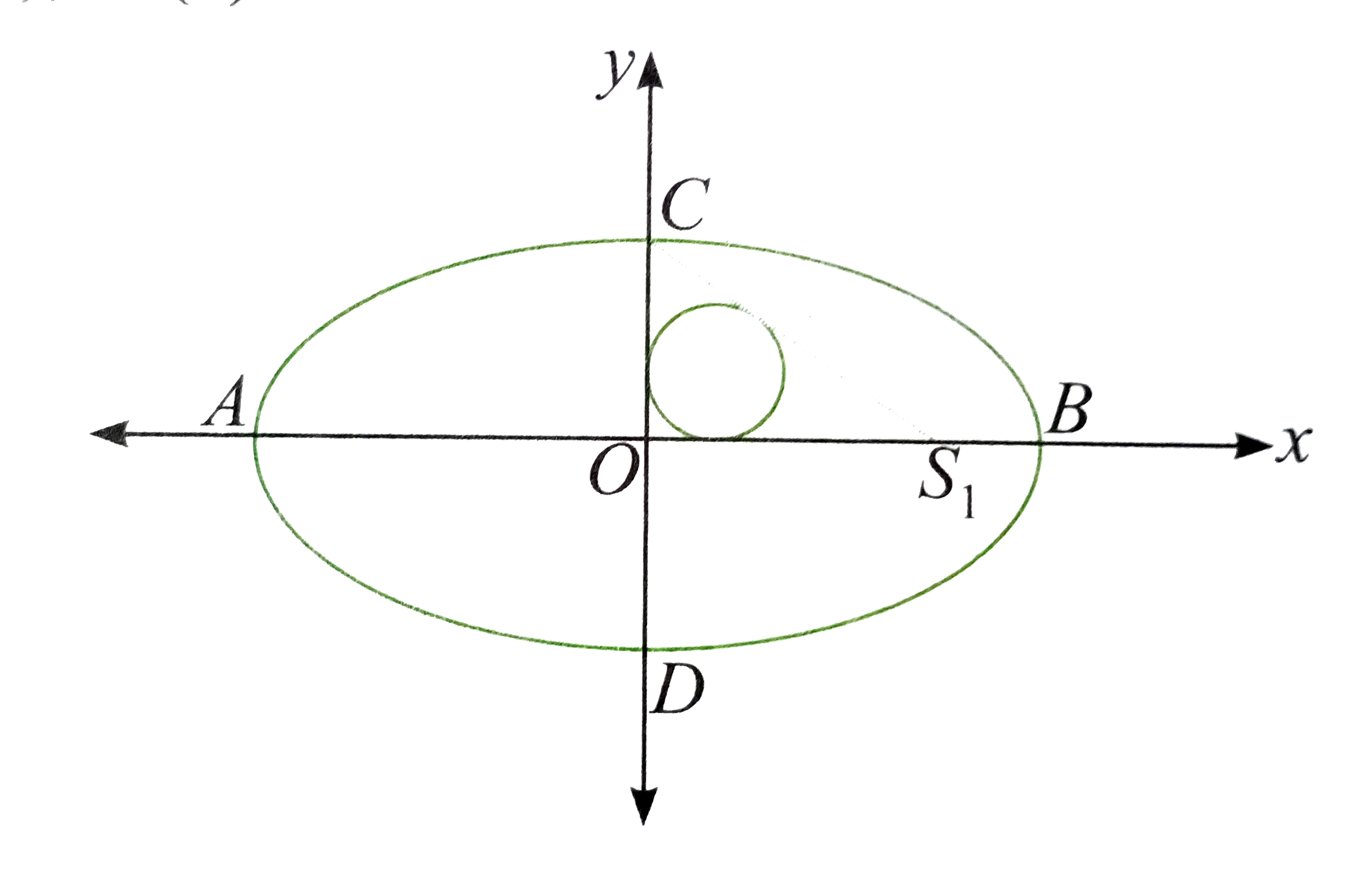
`:.OS_(1)=ae=6,OC=b`
Also,` CS_(1)=a`
`:. "Area of " DeltaOCS_(1)=(1)/(2)=(OS_(1))xx(OC)=3b`
`:.` Semi-perimeter of `DeltaOCS_(1)=(1)/(2)=(OS_(1)+OC+CS_(1))`
`=(1)/(2)(6+a+b) " "(1)`
`:.` In radius of `DeltaOCS_(1) ", "( "Using" r=(Delta)/(S))`
=` (3b)/((1)/(2)(6+a+b))=1" "("Using"r=(Delta)/(S))`
`or 5b=6+a" "(2)`
Also, `b^(2)=a^(2)-a^(2)e^(2)=a^(2)-36" "(3)`
From (2), we get
`25(a^(2)-36)=36+a^(2)+12a`
`or 2a^(2)-a-78=0`
`a=(13)/(2),-6`
`:. a=(13)/(2) and b=(5)/(2)`
Area or ellipse `=piab=(65pi)/(4)` sq. unit
Perimeter of `DeltaOCS_(1)=6+a+b=6+(13)/(2)+(5)/(2)=15` units
The equation of director circle is
`x^(2)+y^(2)=a^(2)+b^(2)`
or `x^(2)+y^(2)=(97)/(2)`