Which of the following statement(s) is/are TRUE?
A
Theren are infinite positive integral values of a for which (13x−1)2+(13y−2)2=(5x+12−1a)2 represents an ellipse
B
The minimum distance of a point (1,2) from the ellipse4x2+9y2−36y+4=0 is 1.
C
If from a point P(0,α) two normals other thn the axes are drawn to the ellipse x225+y216=1 , hen |α|<9/4
D
If the length of the latus rectum of the ellipse is one -third of its major axis, then its eccentrticity is equal to 1√3
Video Solution
Text Solution
The given equation is
(x−113)2+(y−213)2=1a2=1a2(5x+12y−113)2
It represents and ellipse if
1a2<1ora2>1ora>1
(2) 4x2+8x+9y2−36y=−4
or 4(x2+2x+1)+9(y2−4y)+4)=36
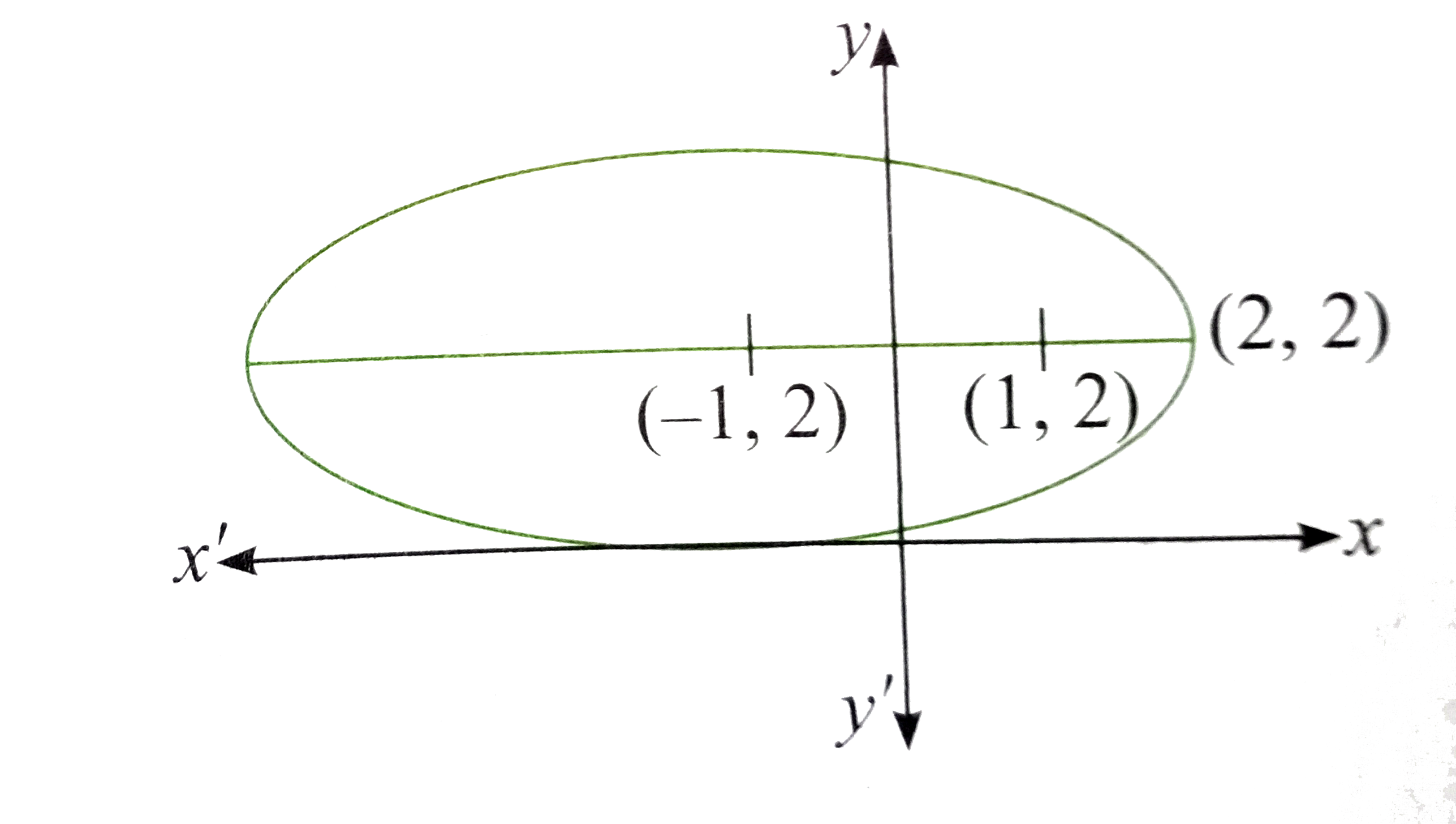
or (x+1)29+(y−2)24=1
Hence, (-1,2) is center and (1,2) lies on the major axis.
Then the required minimum distance is 1.
The equation of normal at P(θ) is 5secθx−4cosecθy=25−16 , and it passes through P(o,α). Therefore,
α=−94cosecθ
=−94sinθ
or|α|<94
2b2a=2a3
or 3b2=a2(1−e2) , we have 1=3(1−e2)ore=√2/3
|
Similar Questions
Knowledge Check
Which of the following statements is true ?
A|10−4|=|10|±4∣BAdditive inverse of -5 is 5C−1 lies on the right of 0 on the number lineD−7 is greater than −3.Which of the following statements is true ?
A−13>−8−(−6)B−5−4>−12+2C(−8)−3=(−3)−(−8)D(−15)−(−22)<(−22)−(−15)Which of the following statements is true ?
AA mixture of enantiomers can be separated on the basis of difference in their boiling points (by a method called fractional distillation)BA mixture of enantiomers can be separated on the basis of difference in their solubility in any solventCA mixture of enantiomers can be separated by converting them into diastereomers by reacting them with an optically active reagentDA mixture of enantiomers can be separated by passing plane polarised through their solution
Which of the following statement(s) is/are with true ?
View SolutionWhich of the following statement(s) is/are with true ?
View SolutionWhich of the following statements (s) is/are not true about the diagonal relationship of Be and Al?
View SolutionWhich of the following statements is true?
View SolutionWhich of the following statements is true?
View Solution