Let P be any point on a directrix of an ellipse of eccentricity e,S be the corresponding focus, and C the center of the ellipse. The line PC meets the ellipse at A. The angle between PS and tangent a A is α . Then α is equal to tan−1e (b) π2 tan−1(1−e2) (d) none of these
tan−1e
π/2
tan−1(1−e2)
none of these
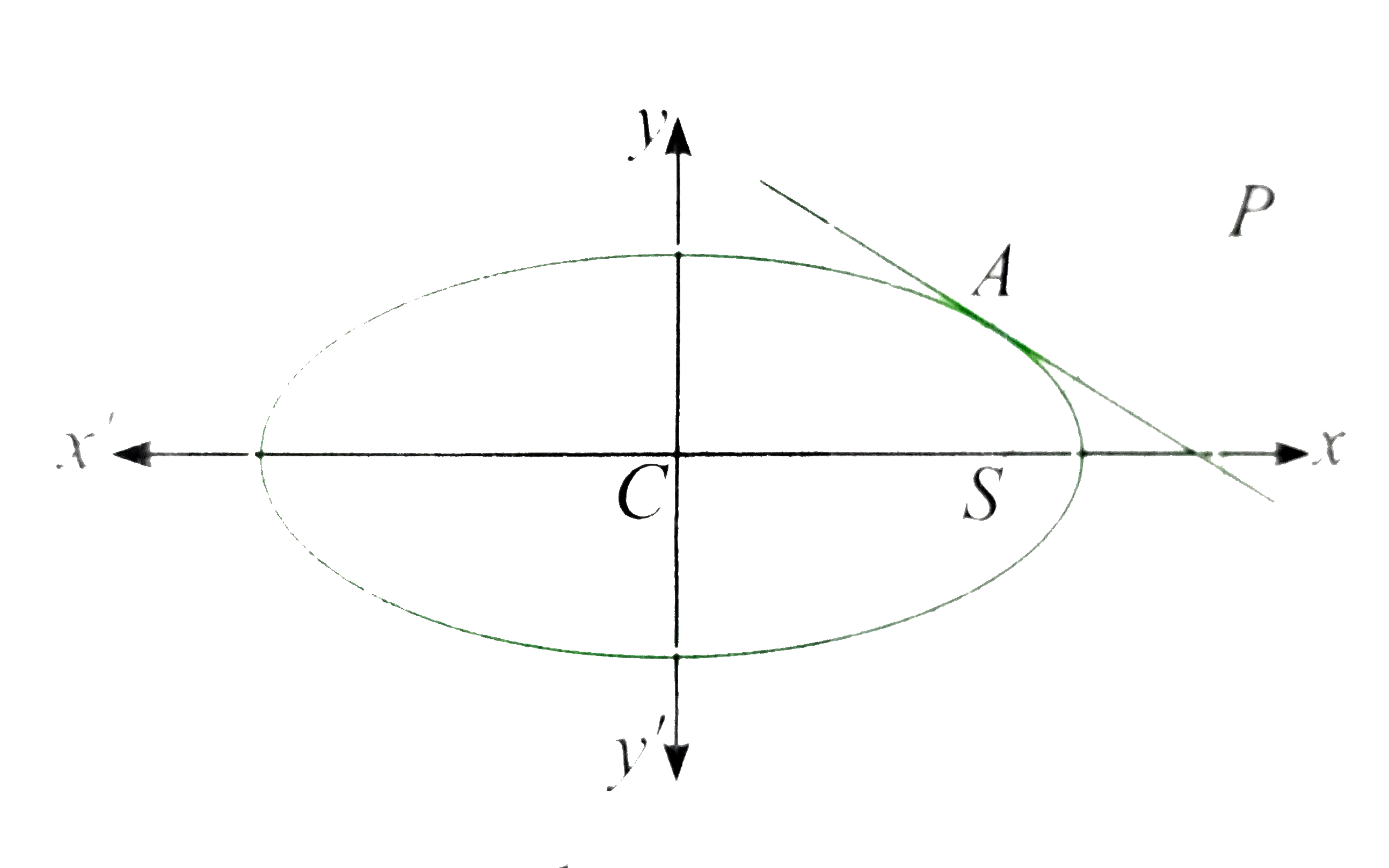
Let the ellipse be
x2a2+y2b2=1
and let A≡(acosθ,bsinθ)
The equation of AC will be
y=batanθx
Solving with x=a/e, we get
P≡(aebetanθ)
Slop of tangent at A=−batanθ
Slope of PS=betanθae−ae=btanθa(1−e2)=abtanθ
So, α=π2
Similar Questions
The focus and corresponding directrix of an ellipse are (3, 4) and x+y−1=0 respectively. If the eccentricity of the ellipse is 12, then the coordinates of the centre of the ellipse are
View SolutionThe focus of an ellipse is (-1, -1) and the corresponding directrix is x−y+3=0. If the eccentricity of the ellipse is 1/2, then the coordinates of the centre of the ellipse, are
View SolutionLet P be a point on the ellipse x2a2+y2b2=1 of eccentricity e. If A,A' are the vertices and S,S are the foci of the ellipse, then find the ratio area PSS'' : area APA′.
View SolutionFind the equation of the ellipse whose focus is (1,−2), the corresponding directrix x−y+1=0 and eccentricity 23.
View SolutionP is the point on the ellipse isx216+y29=1andQ is the corresponding point on the auxiliary circle of the ellipse. If the line joining the center C to Q meets the normal at P with respect to the given ellipse at K, then find the value of CK.
View SolutionLet S=(3,4) and S'=(9,12) be two foci of an ellipse. If the coordinates of the foot of the perpendicular from focus S to a tangent of the ellipse is (1, -4) then the eccentricity of the ellipse is
View SolutionAB and CD are two equal and parallel chords of the ellipse x2a2+y2b2=1. Tangents to the ellipse at A and B intersect at P and tangents at C and D at Q. The line PQ
View SolutionObtain the equation of the ellipse whose focus is the point (-1, 1), and the corresponding directrix is the line x−y+3=0, and the eccentricity is 12.
View SolutionFor the ellipse x29+y24=1. Let O be the centre and S and S' be the foci. For any point P on the ellipse the value of PS.PS'd29 (where d is the distance of O from the tangent at P) is equal to
View SolutionLet the distance between a focus and the corresponding directrix of an ellipse be 8 and the eccentricity be 12 . If the length of the minor axis is k, then √3k2 is ____________
View Solution
