Tangents are drawn to the ellipse x2a2+y2b2=1,(a>b), and the circle x2+y2=a2 at the points where a common ordinate cuts them (on the same side of the x-axis). Then the greatest acute angle between these tangents is given by tan−1(a−b2√ab) (b) tan−1(a+b2√ab) tan−1(2ab√a−b) (d) tan−1(2ab√a+b)
tan−1(a−b2√ab)
tan−1(a+b2√ab)
tan−1(2ab2√a−b)
tan−1(2ab2√a+b)
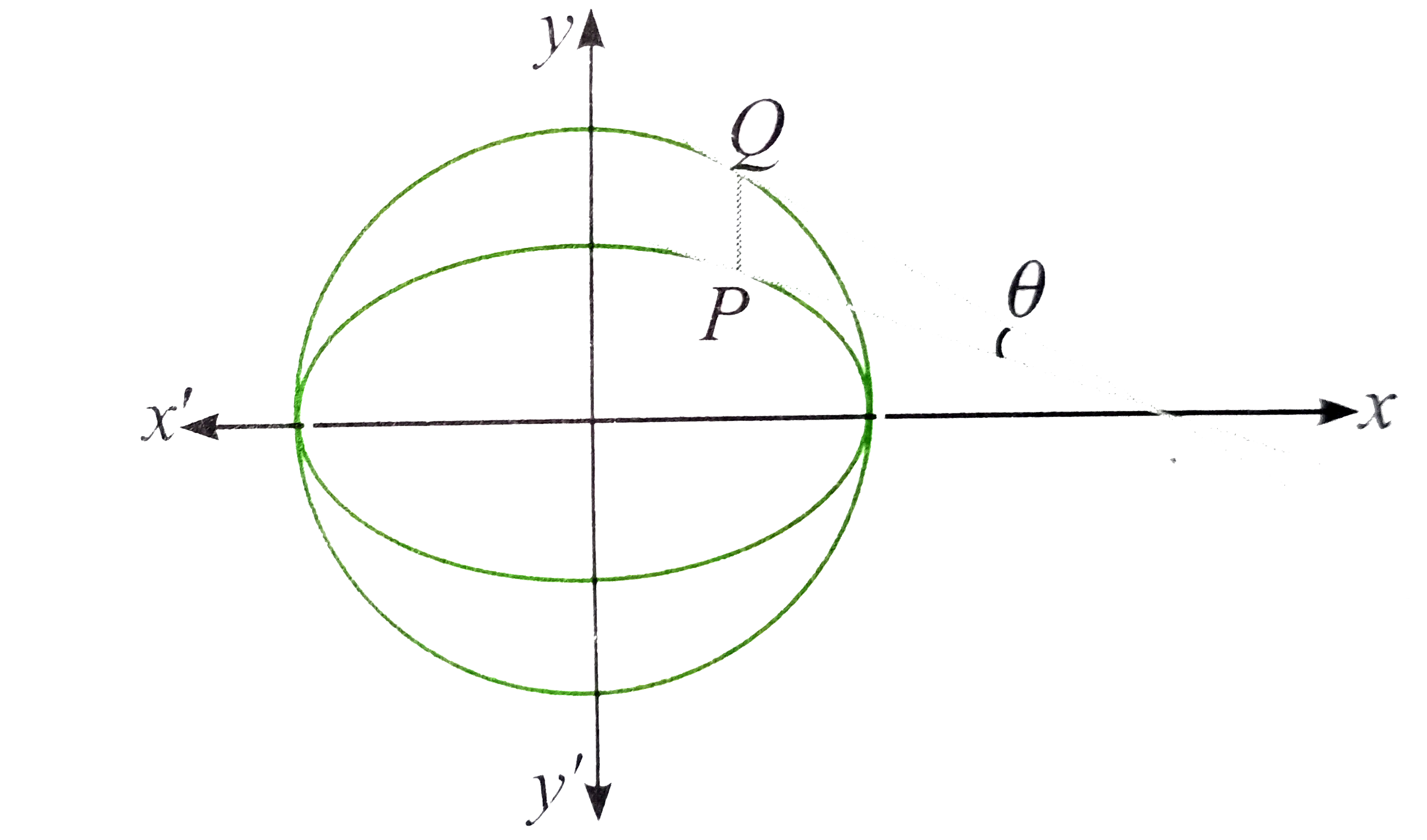
Tanent to the ellipse at P(acosα,bsinα) is xacosα+ybisnα=1 (1)
Tangent to the circle at Q(acos,α,asinα) is cosax+sinαy=a (2)
Now, the angle between the tangents is θ. Then, tanθ=∣∣
∣
∣∣−bacotα−(−cotα)1+(−bacotα)(−cotα)∣∣
∣
∣∣
=∣∣
∣
∣∣cosα(1−ba)1+bacot2α∣∣
∣
∣∣=∣∣∣a−batanα+bcotα∣∣∣
=∣∣
∣
∣∣a−b(√atanα−√bcotα)2+2√ab∣∣
∣
∣∣
Now, the greatest value of the above expression is ∣∣∣a−b2√ab∣∣∣ when √tanα=√btanα. Therefore,
θmaximum=tan−1(a−b2√ab)
Similar Questions
Tangents are drawn to the ellipse x2a2+y2b2=1,(a>b), and the circle x2+y2=a2 at the points where a common ordinate cuts them (on the same side of the x-axis). Then the greatest acute angle between these tangents is given by (A) tan−1(a−b2√ab) (B) tan−1(a+b2√ab) (C) tan−1(2ab√a−b) (D) tan−1(2ab√a+b)
View SolutionIf a tangent of slope13 of the ellipse x2a2+y2b2=1(a>b) is normal to the circle x2+y2+2x+2y+1=0 then
View SolutionProve that the ellipse x2a2+y2b2=1 and the circle x2+y2=ab intersect at an angle tan−1(|a−b|√ab).
View SolutionA normal to parabola, whose inclination is 30∘, cuts it again at an angle of (a) tan−1(√32) (b) tan−1(2√3) (c) tan−1(2√3) (d) tan−1(12√3)
View SolutionTangents are drawn to the ellipse from the point (a2√a2−b2,√a2+b2)) . Prove that the tangents intercept on the ordinate through the nearer focus a distance equal to the major axis.
View SolutionA tangent is drawn to the ellipse to cut the ellipse x2a2+y2b2=1 and to cut the ellipse x2c2+y2d2=1 at the points P and Q. If the tangents are at right angles, then the value of (a2c2)+(b2d2) is
View SolutionIf 3tan−1(12+√3)−tan−11x=tan−113, then x is equal to 1 (b) 2 (c) 3 (d) √2
View SolutionFind the equations of the tangent and the normal to the curve x2a2−y2b2=1 at (√2a, b) at indicated points.
View SolutionThe slopes of the common tangents of the ellipse x24+y21=1 and the circle x2+y2=3 are ±1 (b) ±√2 (c) ±√3 (d) none of these
View SolutionIf a,b,c>0 and s=a+b+c2, prove that tan−1√2asbc+tan−1√2bsca+tan−1√2csab=π
View Solution