Question

Tangents ${\displaystyle PQandPR}$
are drawn
at the extremities of the chord of the ellipse ${\displaystyle \frac{x^2}{16}+\frac{y^2}{9}=1}$
, which get bisected at point ${\displaystyle P(1,1)\stackrel{.}{}}$
Then find
the point of intersection of the tangents.

Answer

`((144)/(25),(144)/(25))`

Explanation

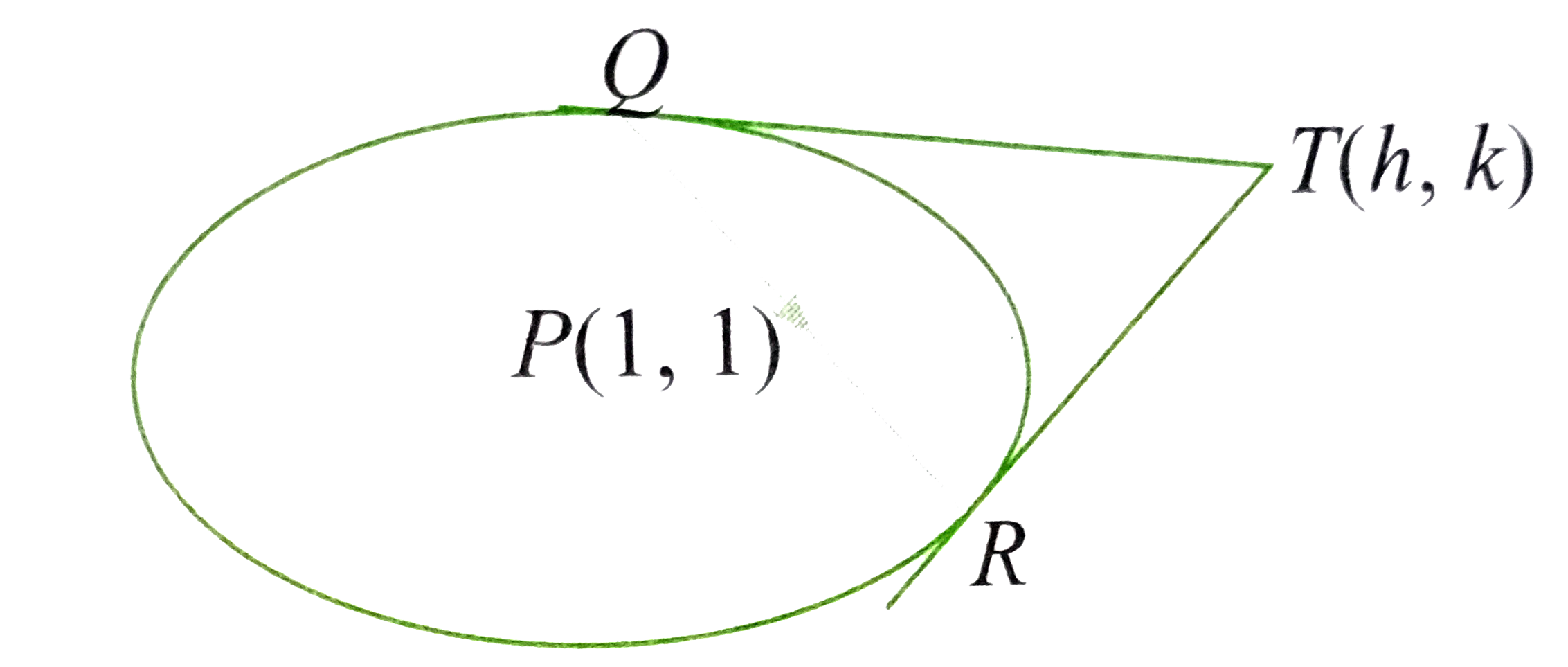
Eqution of chord having midpoint P(1,1) is
`(1*x)/(16)+(1*y)/(9)-1=(1)/(16)+(1)/(9)-1`
or `(x)/(16)+(y)/(9)=(25)/(144)`
`or 9x+16y=25" (1)`
Also, line QR is chord of contact w.r.t. point (h,k).
It equations is
`(hx)/(16)+(ky)/(9)=1`
or `9hx+16ky=144 " "(2)`
Equatiosn (1) and (2) represent the same stragith line.
`:. (9h)/(9)=(16k)/(16)=(144)/(25)`
`rArr(h,k)-=((144)/(25),(144)/(25))`