Find the point (α,)β on the ellipse 4x2+3y2=12, in the first quadrant, so that the area enclosed by the lines y=x,y=β,x=α , and the x-axis is maximum.
The correct Answer is:(3/2,1)
The equation of the ellipse is x23+y24=1
Let point P be (√3cos,θ,2sinθ),θ∈(0,π/2)
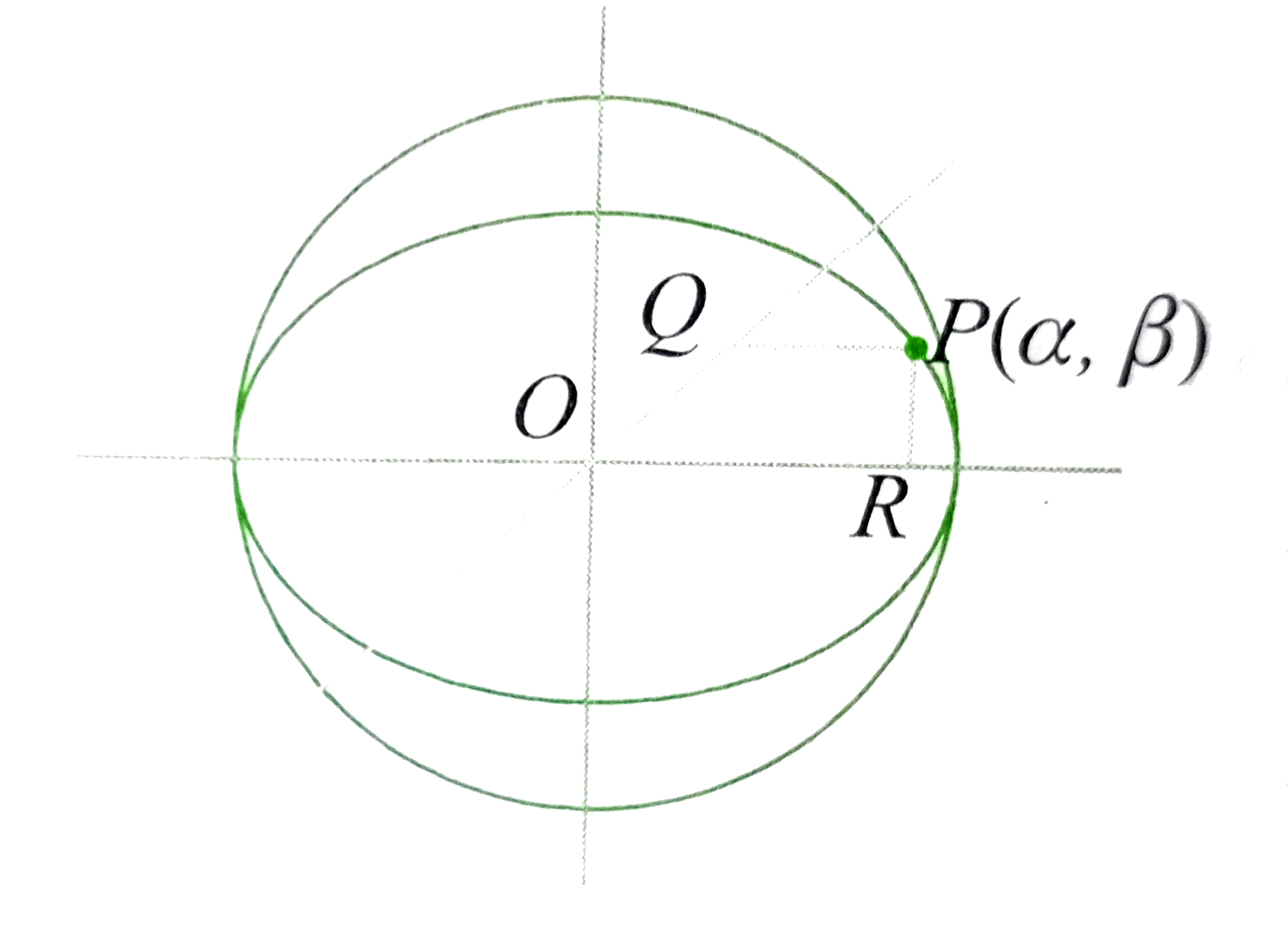
Clearly, line PQ is y=sinθ , line PR is x=√3cosθ, line OQ is y=x, and Q is (2sinθ,2sinθ),
Z= Area of region PQORP (tranpezium)
=12(OR+PQ)PR
=12(√3cosθ+√3cosθ−2sinθ)2sinθ
=(2√3cosθsinθ−2sin2θ)
=(√3sin2θ+cos2θ−1)
=2cosθ(2θ−π3)−1
which is maximum when cos(θ−π3) is maximum
∴2θ−π3=0
or θ=π6
Hence, point P is (3/2,1)
Similar Questions
Find the area of the region enclosed by the curves
y=x2−4x+3 and the x-axis
View SolutionFind the area of the region enclosed by the parabola x2=y , the line y = x + 2 and the x-axis.
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 the line x=√3y and x-axis , is
View SolutionFind the area of the region bouonded by y2=4x,x=1,x=4 and x-axis in the first quadrant.
View SolutionFind the area of the region bounded by y=√x, x=2y+3 in the first quadrant and x-axis.
View SolutionI If a point (α,β) lies on the circle x2+y2=1 then the locus of the point (3α.+2,β), is
View SolutionFind the area bounded by the curve 2x2−y=0 and the lines x=3,y=1 and the x-axis all in first quadrant.
View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
View SolutionFind the area enclosed by the parabola 4y=3x2 and the line 2y=3x+12.
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View Solution