Question

An ellipse is drawn with major and minor axis of length $10$ and $8$ respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is

Answer

2

Explanation

Givemn ellipse
`(x^(2))/(25)+(y^(2))/(16)=1`
`:. E^(2)=1-(16)/(25) or e=(3)/(5)`

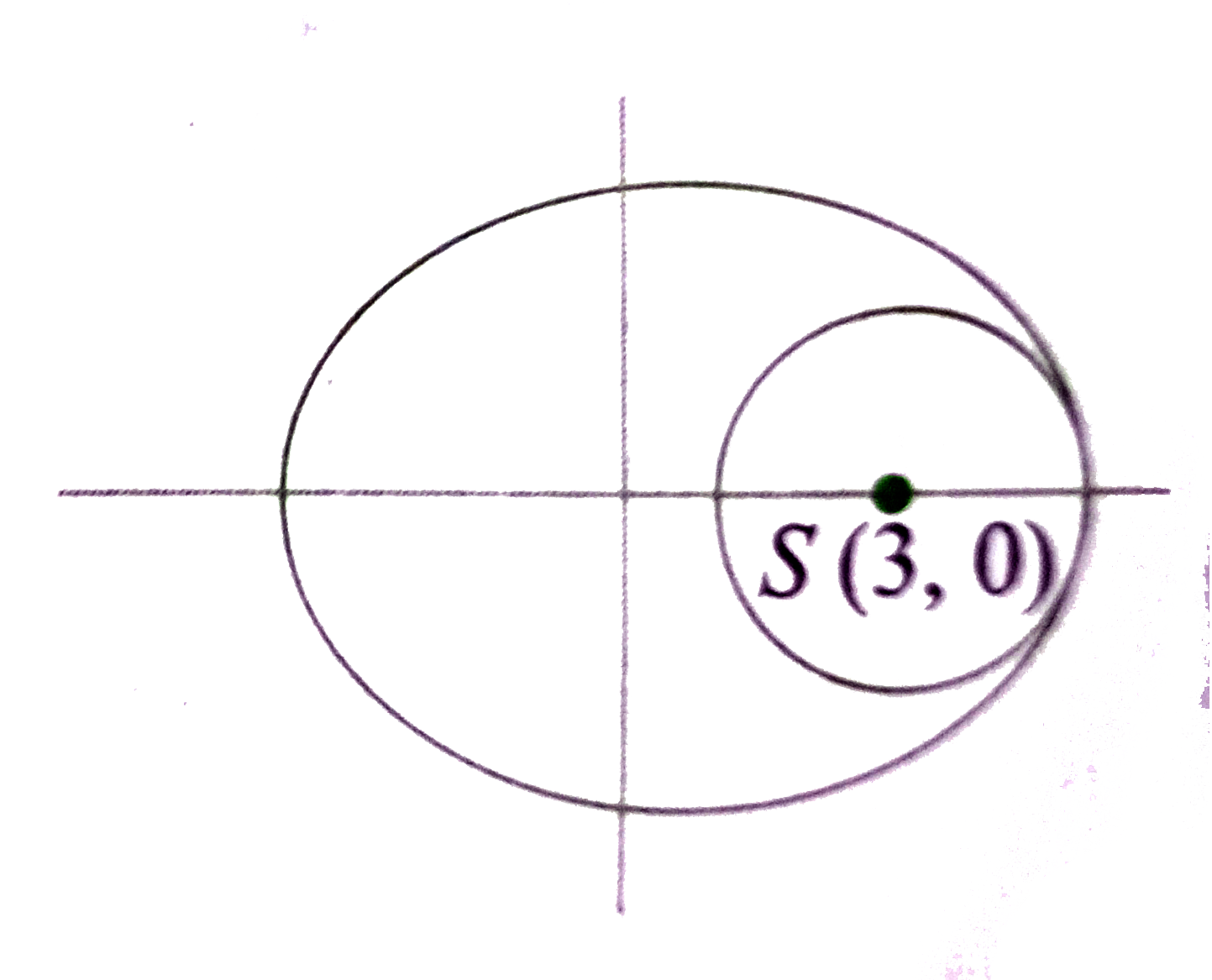
then foci are `(+-ae,0) -= (+-3,0)`
Now, the circle having center (3,0) is
`(x-3)^(2)+y^(2)=r^(2)`
Eliminating `y^(2)` from (1) and (2), we get
`16x^(2)+25r^(2)-25(x^(2)-6x+9)=400`
or `-9x^(2)+150x+25r^(2)-625=0`
since the circle touches the ellipse, the above equation, has equal roots. Hence `D=0,i.e.,22500+36(25r^(2)-625)=0`, which is not possible
Then the circle will touche the ellipse at the end of the major axis, (5,0) Hence, the radius is 2