The circle passing through the point (−1,0) and touching the y-axis at (0,2) also passes through the point.
(−5,2)
(2,−5)
(5,−2)
(−2,5)
The correct Answer is:C
Let centre C(3,k)
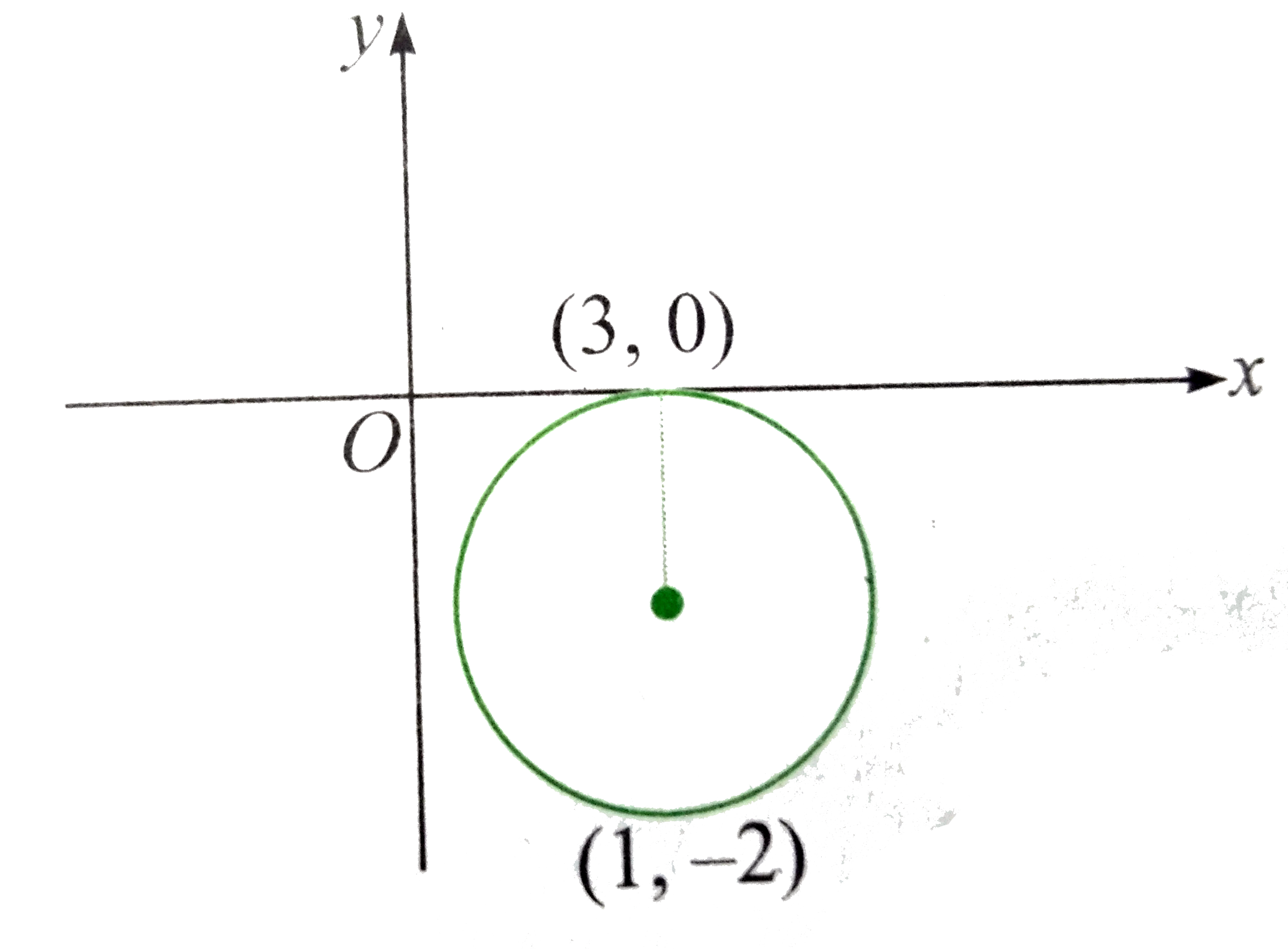
As circle touches CX -axis.
⇒r=k
So, circle is (x−3)2+(y−k)2=k2
Given that it passes through (1,−2)
4+(k+2)2=k2
⇒4+k2+4k+4=k2
⇒4k=−8
⇒k=−2
Circle is (x−3)2+(y+2)20=4
Obviously(5,−2) satisfy the above equation.
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:JEE ADVANCED (Single Correct Answer Type)
Explore 3 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:LINKED COMPREHENSION TYPE (For problem 1 and 2)
Explore 2 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:ARCHIVES (JEE MAIN)
Explore 1 Video
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
The circle passing through (1, -2) and touching the axis of x at (3, 0) also passes through the point (1) (2, -5) (2) (5, -2) (3) (-2, 5) (4) (-5, 2)
View SolutionThe circle passing through (1, -2) and touching the axis of x at (3, 0) also passes through the point
View SolutionThe circle passing through the points (1, t), (t, 1) and (t, t) for all values of t passes through the point
View SolutionThe common chord of the circle x2+y2+6x+8y−7=0 and a circle passing through the origin and touching the line y=x always passes through the point. (a) (−12,12) (b) (1, 1) (c) (12,12) (d) none of these
View SolutionFind the equation of the circle passing through the point ( 2, 3) and touching the line 2x+3y=4 at the point ( 2, 0)
View SolutionFind the equation of the circle passing through the points A(4,3).B(2,5) and touching the axis of y. Also find the point P on the y-axis such that the angle APB has largest magnitude.
View SolutionStatement-1: The centre of the circle passing through the points (0, 0), (1, 0) and touching the circle C:x2+y2=9 lies inside the circle.
Statement-2: If a circle C1 passes through the centre of the circle C2 and also touches the circle, the radius of the circle C2 is twice the radius of circle C1
View SolutionA variable circle passes through the point A(a,b) and touches the x-axis. Show that the locus of the other end of the diameter through A is (x−a)2=4by.
View SolutionA variable circle passes through the point A(a,b) and touches the x-axis. Show that the locus of the other end of the diameter through A is (x−a)2=4by.
View SolutionA variable circle passes through the point P(1,2) and touches the x-axis. Show that the locus of the other end of the diameter through P is (x−1)2=8y.
View Solution

