Let be real variables satisfying . Let and . Then (a) (b) (c) (d)
The correct Answer is:1,3,4
The center of the circle is .
its radius is 9. distance of the center from the point is . Therefore, and
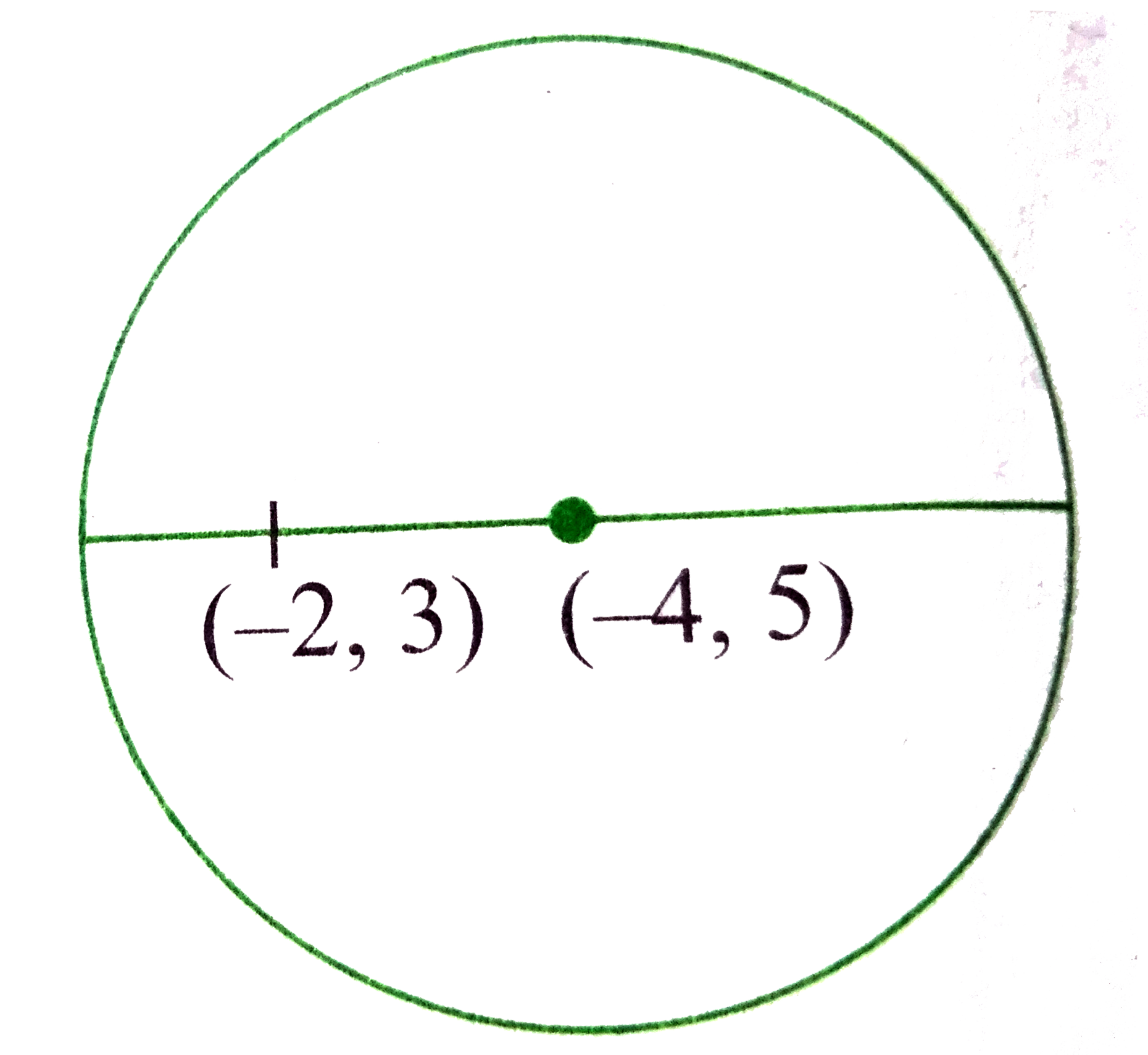
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - For Problems
43 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Excercises (Single Correct Answer Type)
109 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Let x, y be real variable satisfying x2+y2+8x−10y−59=0 Let a=max{(x−3)2+(y−4)2 and b=min{(x−3)2+(y−4)2), then a + b + 2010 is ______ .
View SolutionIf a=max{(x+2)2+(y−3)2}andb=min{(x+2)2+(y−3)2} where x, y satisfying x2+y2+8x−10y−40=0 then :
View Solutionmin[(x1−x2)2+(5+√1−x21−√4x2)2],∀x1,x2∈R, is (a)4√5−1 (b) 3−2√2 (c)√5+1 (d) √5−1
View SolutionThe slopes of the common tangents of the ellipse x24+y21=1 and the circle x2+y2=3 are ±1 (b) ±√2 (c) ±√3 (d) none of these
View SolutionLength of the latus rectum of the parabola √x+√y=√a is (a) a√2 (b) a√2 (c) a (d) 2a
View SolutionIf y=√x+1√x, then dydx at x=1 is a. 1 b. 12 c. 1√2 d. 0
View SolutionIf y={x+√x2+a2}n , then prove that dydx=ny√x2+a2 .
View SolutionIf y=(x+√x2+a2)n,thendydx is (a)ny√x2+a2 (b) −ny√x2+a2 (c)nx√x2+a2 (d) −nx√x2+a2
View SolutionIf y=(x+√x2+a2)n,thendydx is ny√x2+a2 (b) −ny√x2+a2 nx√x2+a2 (d) −nx√x2+a2
View SolutionIf y=(x+√x2+a2)n,thendydx is ny√x2+a2 (b) −ny√x2+a2 nx√x2+a2 (d) −nx√x2+a2
View Solution
