Two circle with radii r1 and r2 respectively touch each other externally. Let r3 be the radius of a circle that touches these two circle as well as a common tangents to two circles then which of the following relation is true
1√a−1√b=1√c
c=2aba+b
1√a+1√b=1√c
c=2ab√a+√b
The correct Answer is:3
To solve the problem, we need to establish a relationship between the radii of three circles: r1, r2, and r3, where r1 and r2 are the radii of two externally touching circles and r3 is the radius of a circle that touches both of these circles as well as a common tangent to both circles.
1. Understanding the Configuration:
- We have two circles with radii r1 and r2 that touch each other externally.
- A third circle with radius r3 touches both of these circles and also touches a common tangent to both circles.
2. Using the Tangent and Circle Properties:
- The distance between the centers of the two circles r1 and r2 is r1+r2.
- The radius r3 of the third circle can be determined using the properties of tangents and circles.
3. Setting Up the Equation:
- By applying the relationship derived from the geometry of the circles, we can express the relationship as:
1√r3=1√r1+1√r2
- This equation arises from the fact that the distance from the center of the third circle to the tangent point is equal to the radius of the third circle.
4. Rearranging the Equation:
- Rearranging the equation gives us:
1√r3=1√r1+1√r2
- This can be rewritten as:
1√r1+1√r2=1√r3
5. Conclusion:
- The relationship derived indicates that option 3 is correct:
1√r1+1√r2=1√r3
Final Answer:
The correct relation is:
1√r1+1√r2=1√r3
- We have two circles with radii r1 and r2 that touch each other externally.
- A third circle with radius r3 touches both of these circles and also touches a common tangent to both circles.
- The distance between the centers of the two circles r1 and r2 is r1+r2.
- The radius r3 of the third circle can be determined using the properties of tangents and circles.
- By applying the relationship derived from the geometry of the circles, we can express the relationship as:
1√r3=1√r1+1√r2
- This equation arises from the fact that the distance from the center of the third circle to the tangent point is equal to the radius of the third circle.
- Rearranging the equation gives us:
1√r3=1√r1+1√r2
- This can be rewritten as:
1√r1+1√r2=1√r3
- The relationship derived indicates that option 3 is correct:
1√r1+1√r2=1√r3
The correct relation is:
1√r1+1√r2=1√r3
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Multiple Correct Anser Type
Explore 29 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Linked Comprehension Type (For Problem 1-3)
Explore 3 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.20
Explore 1 Video
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
Two fixed circles with radii r1andr2,(r1>r2) , respectively, touch each other externally. Then identify the locus of the point of intersection of their direction common tangents.
View SolutionTwo circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
View Solution
Knowledge Check
Two circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.
A32 cmB50 cmC40 cmD30 cm
The circles having radii 1, 2, 3 touch cach other externally then the radius of the circle which cuts three circles orthogonally is
View SolutionThe locus of the centre of a circle which touches two given circles externally is a
View SolutionTwo circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
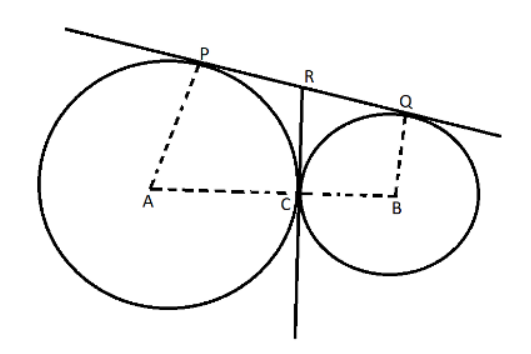
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionTwo circles touch each other externally. The sum of their areas is 74πcm2 and the distance between their centres is 12 cm. Find the diameters of the circle.
View SolutionCircles of radii 3,4,5 touch each other externally . Let P be the point of intersection of tangents of these circles at their points of contact .Show that the distance of P from a point of contact is √5.
View SolutionThe length of a common internal tangent to two circles is 5 and a common external tangent is 15, then the product of the radii of the two circles is :
View Solution

