The locus of centre of a circle which passes through the origin and cuts off a length of 4 units on the line x=3 is
The correct Answer is:y2+6x=13
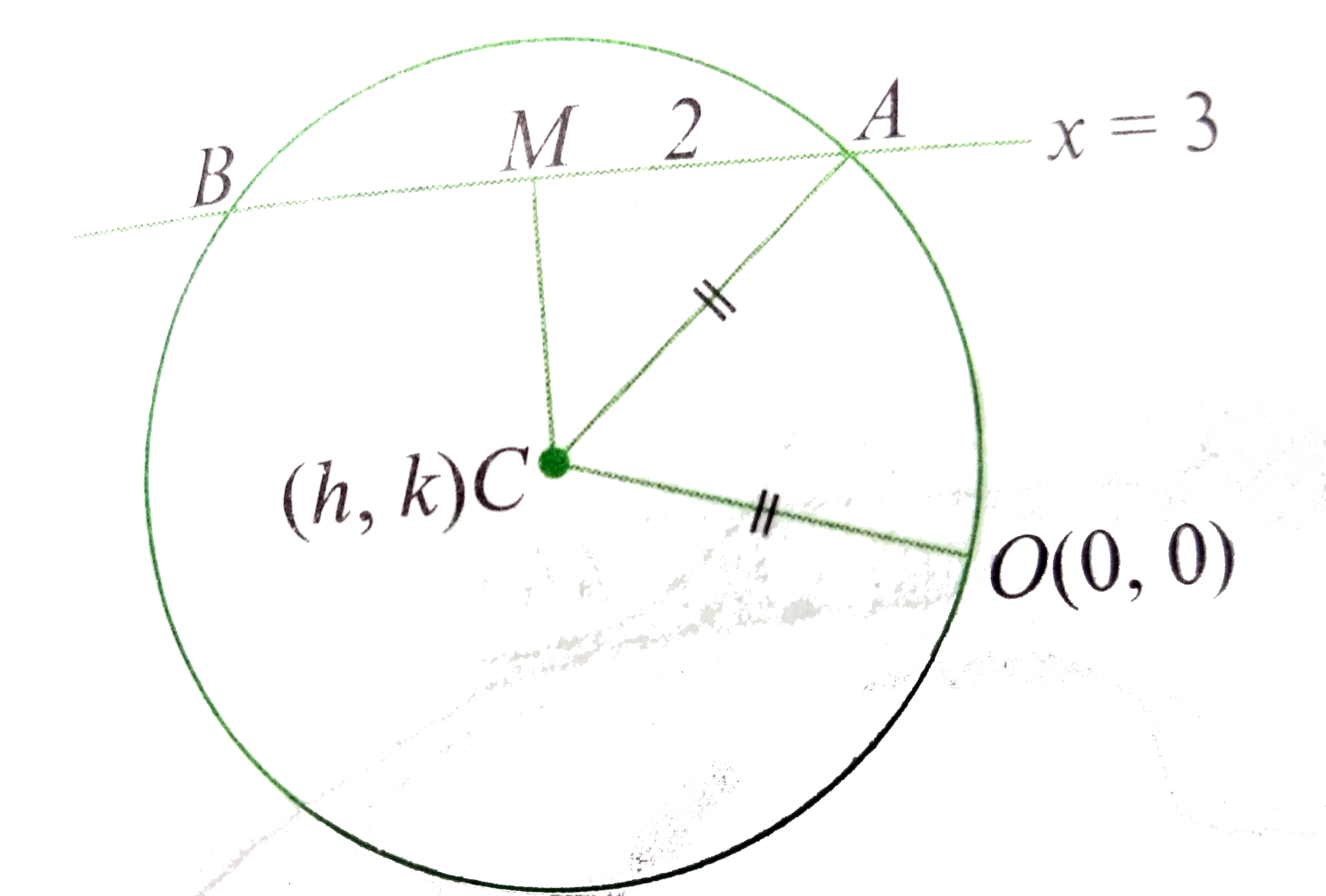
From the figure,
CO=CA
or CO2=CM2+AM2
⇒(h−0)2+(k−0)2=(|h−3|1)2+4
⇒h2+k2=h2−6h+13
or k2=−6h+13
or k2+h=13
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.7
5 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.8
5 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.5
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Find the locus of the centre of a circle which passes through the origin and cuts off a length 2b from the line x=c.
View SolutionFind the locus of the centre of a circle which passes through the origin and cuts off a length 2l from the line x=c.
View SolutionFind the equation of the circle which passes through the origin and cut off equal chords of √2 units from the lines y=xandy=−x.
View SolutionThe locus of the centres of all circles passing through two fixed points.
View SolutionFind the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the circle concentric with the circle x2+y2−6x+12y+15=0 and double of its area.
View SolutionFind the equations of the circles which pass through the origin and cut off chords of length a from each of the lines y=xandy=−x
View SolutionFind the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the x-axis and y-axis respectively.
View SolutionEquation to the circles which pass through the point (2,3) and cut off equal chords of length 6 units along the lines y-x-1=0 and y+x-5=0 is
View SolutionFind the equation of a circle which passes through the origin and whose centre is (a, b).
View SolutionThe equation of the circles which pass through the origin and makes intercepts of lengths 4 and 8 on the x and y-axis respectively are
View Solution
