Question

If $\theta$
is the angle between the two radii (one to each circle) drawn from one
of the point of intersection of two circles $x^2+y^2=a^2$
and ${(x-c)}^2+y^2=b^2,$
then prove that the length of the common chord of the two circles is $\frac{2ab\sin \theta }{\sqrt{a^2+b^2-2ab\cos \theta }}$

Explanation

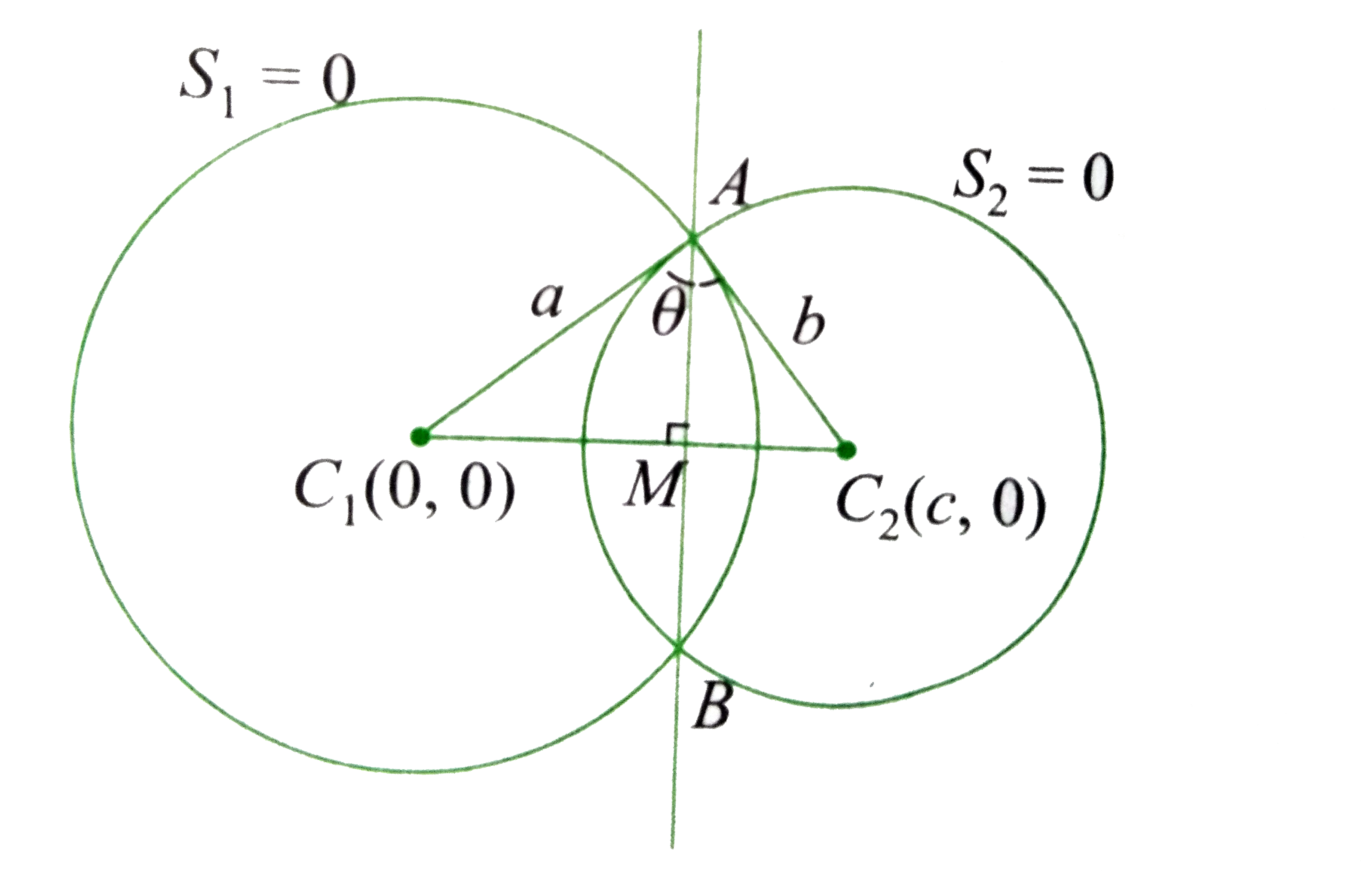
From the figure,
`cos theta =(a^(2)+b^(2)-c^(2))/(2ab)`
`:. c=sqrt(a^(2)+b^(2)-2ab cos theta)= C_(1)C_(2)`
Area of triangle `C_(1)AC_(2)=(1)/(2)ab sin theta=(1)/(2)AM xx C_(2)C_(2)`
`:. AM =(ab sin theta)/(sqrt(a^(2)+b^(2)-2ab cos theta))`
`:.` Length of common chord, `AB=2AM=(2ab sin theta)/(sqrt(a^(2)+b^(2)-2ab cos theta))`