Find the equation of the tangent at the endpoints of the diameter of circle (x−a)2+(y−b)2=r2 which is inclined at an angle θ with the positive x-axis.
Diameter makes an angle θ with x-axis.
So, the slope of diameter is tanθ
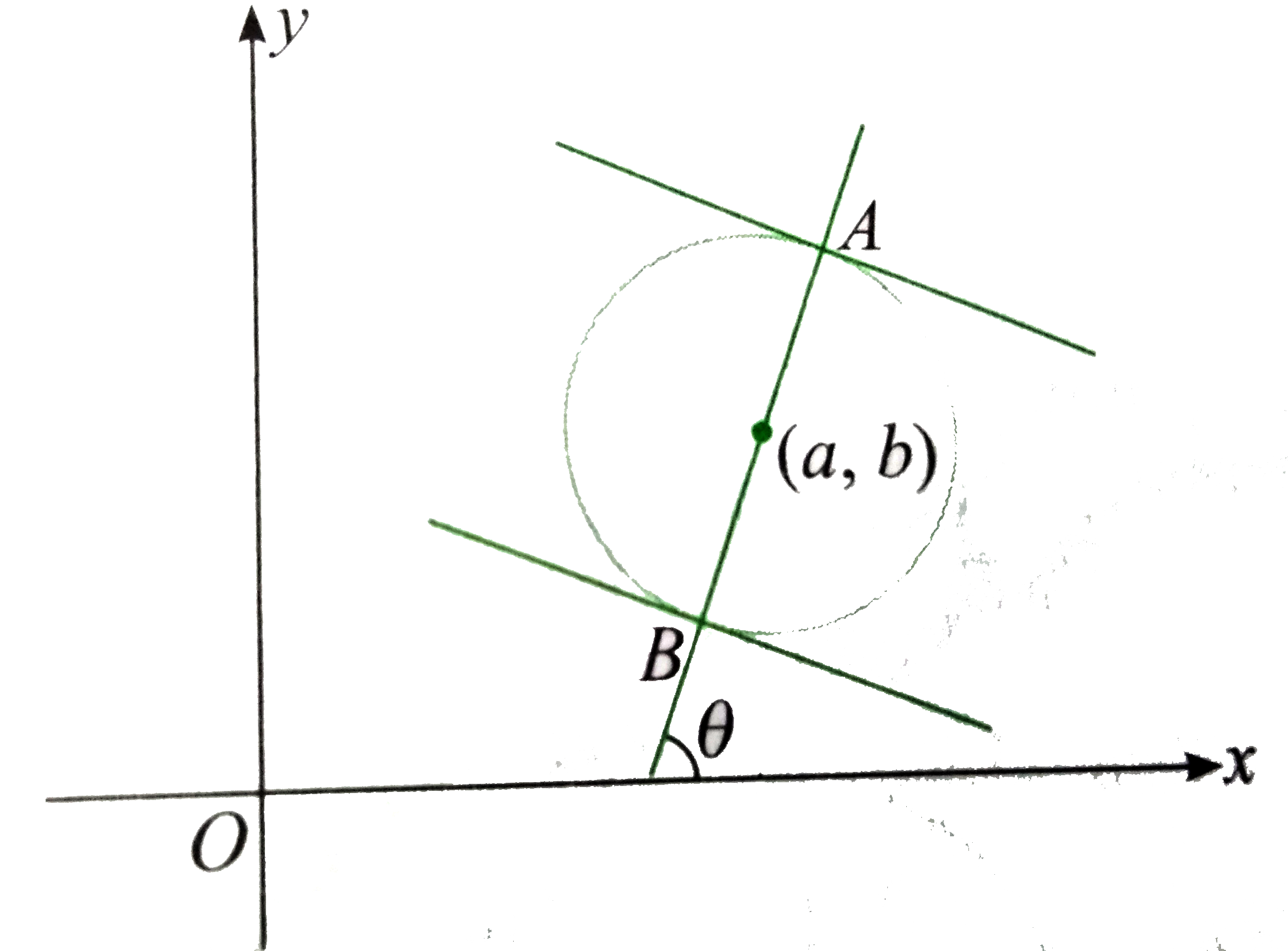
Let this diameter meet the circle at points A and B.
Thus, the coordinates of A and B are given by (a±rcosθ,b±rsinθ)
Therefore, equations of tangents at points A and B are given by
(x−a)(a±rcosθ−a)+(y−b)(b±rsinθ−b)=r2
or ±(x−a)cosθ±r(y−b)sinθ=r
or (x−a)cosθ+(y−b)sinθ=±r
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Examples
13 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Find the equation of the line which intercepts a length 2 on the positive direction of the x-axis and is inclined at an angle of 135∘ with the positive direction of y-axis .
View SolutionIf θ is the angle between the lines given by the equation 6x2+5xy−4y2+7x+13y−3=0 , then find the equation of the line passing through the point of intersection of these lines and making an angle θ with the positive x-axis.
View SolutionIf θ is the angle between the lines given by the equation 6x2+5xy−4y2+7x+13y−3=0 , then find the equation of the line passing through the point of intersection of these lines and making an angle θ with the positive x-axis.
View SolutionFind the equation of the tangent to the curve (1+x2)y=2−x, where it crosses the x-axis.
View SolutionFind the equation of the tangent to the curve (1+x2)y=2−x, where it crosses the x-axis.
View SolutionFind the equation of tangent and normal at
(3,2) of the circle x2+y2−3y−4=0.
View SolutionThe points of contact of tangents to the circle x2+y2=25 which are inclined at an angle of 30∘ to the x-axis are
View SolutionFind the equations of the tangents to the circle x2+y2=25 inclined at an angle of 60∘ to the x-axis.
View SolutionEquation of the tangent to the circle x2+y2=3, which is inclined at 60∘ with the x-axis is
View SolutionFind the equation of the tangent at the
point 30∘ (parametric value of θ) of the
circle is x2+y2+4x+6y−39=0.
View Solution
