$P$ is the variable point on the circle with center at $C \dot{C} A$ and $C B$ are perpendiculars from $C$ on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle $P A B$ is a circle with center at the centroid of triangle $C A B$ and radius equal to the one-third of the radius of the given circle.

Video Solution

Text Solution

Verified by Experts

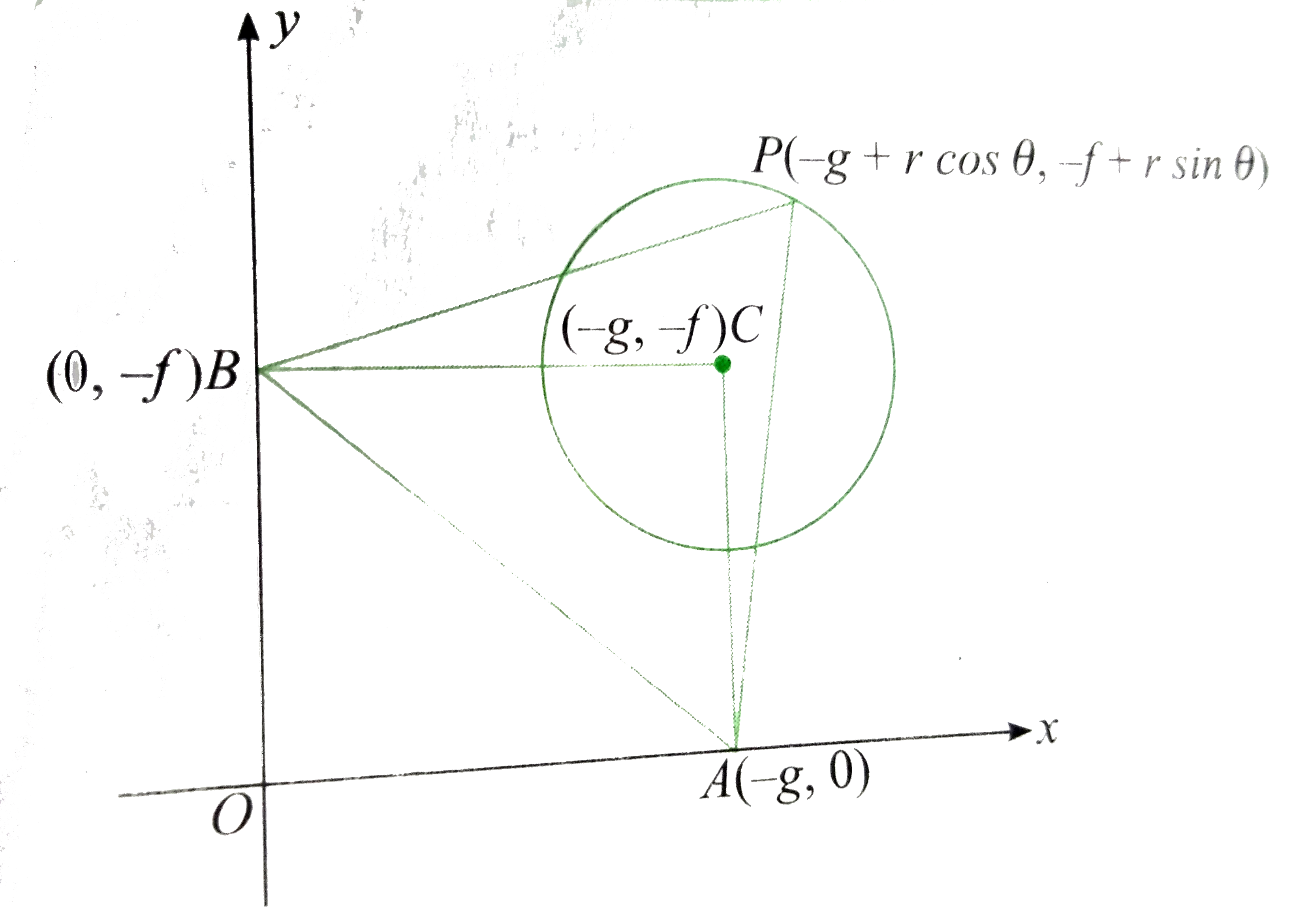
Let the circle be $x^{2} + y^{2} + 2 g x + 2 f y + c = 0$ .
Let the centroid of triangle PAB be (h,k). ltBRgt $∴ 3 h = 2 g + r \cos θ$
and $3 k = - 2 f + r \sin θ$
$\Rightarrow {(2 h + 2 g)}^{2} + {(3 k + 2 f)}^{2} = r^{2}$
$\Rightarrow {(x + 2 g / 3)}^{2} + {(y + 2 / 3)}^{2} = r^{2} / 9$
This is the required locus which is a circle.
Centre of the circle is $(- 2 g / 3, - 2 f / 3)$ which is centroid of the triangle CAB and radius $(r / 3)$ which is one-third of the radius of the given circle.

Updated on:21/07/2023