A circle with center at the origin and radius equal to a meets the axis of $x$ at $A a n d B . P (α)$ and $Q (β)$ are two points on the circle so that $α - β = 2 γ$ , where $γ$ is a constant. Find the locus of the point of intersection of $A P$ and $B Q .$

Video Solution

Text Solution

Verified by Experts

Let

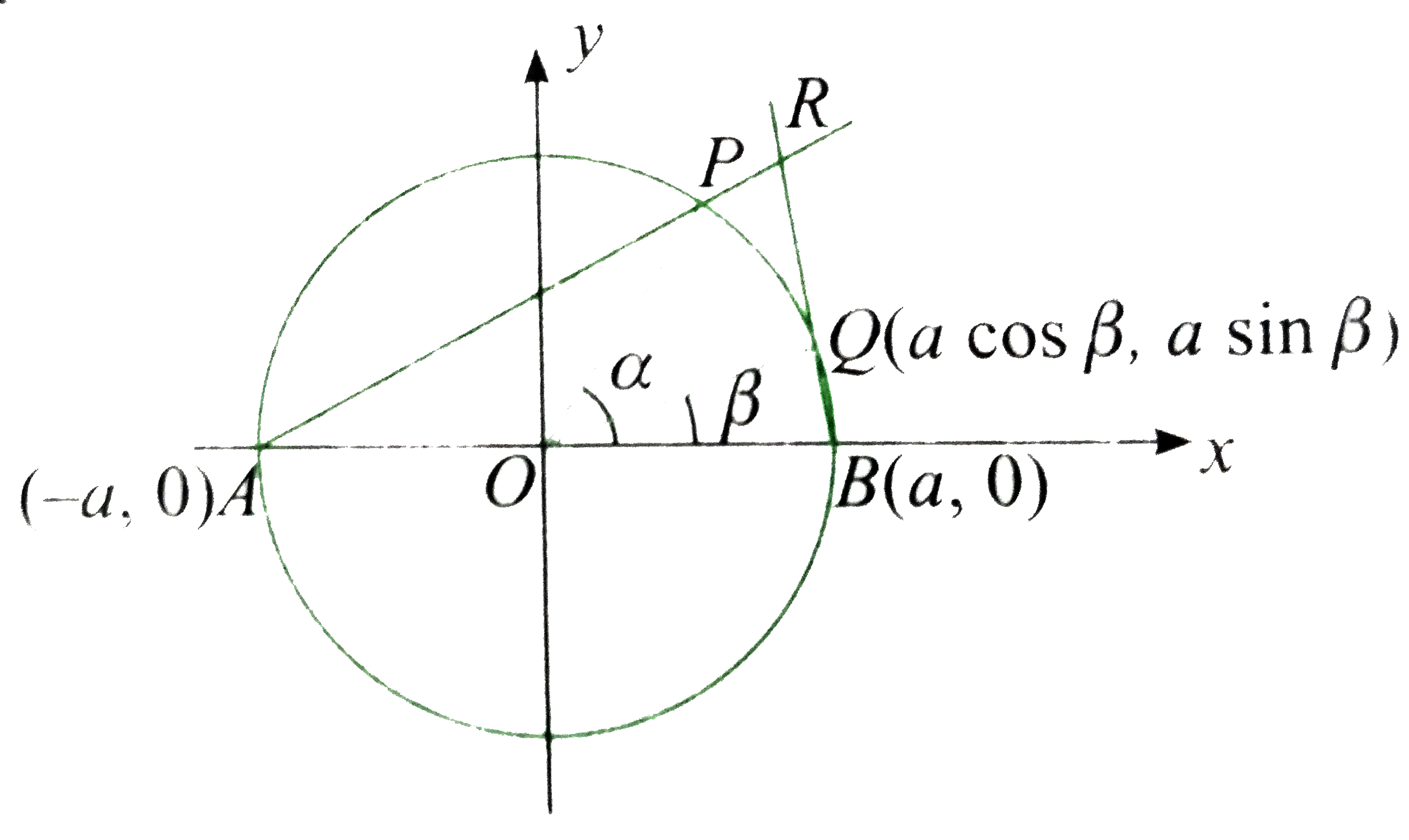
The coordinates of A are ( -a,0) and that of P are $(a cos α, a sin α)$ .
Therefore, the equation of AP is
$y = \frac{a sin α}{a (cos α + 1)} (x + a)$
or $y = tan . \frac{α}{2} (x + a)$ (1)
Similarly, the equationof BQ is
$y = \frac{a sin β}{a (cos β - 1)} (x - a)$
or $y = - cot . \frac{β}{2} (x - a)$ (2)
We now eliminate $α$ and $β$ from (1) and (2). Therefore,
$tan . \frac{α}{2} = \frac{y}{a + x}, tan . \frac{β}{2} = \frac{a - x}{y}$
Now, $α - β = 2 γ \Rightarrow γ = \frac{α}{2} - \frac{β}{2}$
$∴ tan γ = \frac{tan . \frac{α}{2} - tan . \frac{β}{2}}{1 + tan . \frac{α}{2} tan . \frac{β}{2}} = \frac{\frac{y}{a + x} - \frac{a - x}{y}}{1 + \frac{y}{a + x} . \frac{a - x}{y}}$
or $tan γ = \frac{y^{2} - (a^{2} - x^{2})}{(a + x) y + (a - x) y}$
$= \frac{x^{2} + y^{2} - a^{2}}{2 a y}$
or $x^{2} + y^{2} - 2 a y tan γ = a^{2}$

Updated on:21/07/2023

The distance of the point P $(α, β, γ)$ from x-axis is
A $| α |$
B $\sqrt{α^{2} + β^{2}}$
C $\sqrt{β^{2} + γ^{2}}$
D $\sqrt{γ^{2} + α^{2}}$
The distance of the point $P (α, β, γ)$ from y-axis is
A $β$
B $| β |$
C $| β | + | γ |$
D $\sqrt{γ^{2} + α^{2}}$
The reflection of the point $P (α, β, γ)$ in the xy-plane is
A $(α, β, 0)$
B $(0, 0, γ)$
C $(- α, - β, γ)$
D $(α, β, - γ)$