Two vertices of an equilateral triangle are $(- 1, 0)$ and (1, 0), and its third vertex lies above the x-axis. The equation of its circumcircel is ____________

Video Solution

Text Solution

Verified by Experts

We have equilateral triangle ABC.

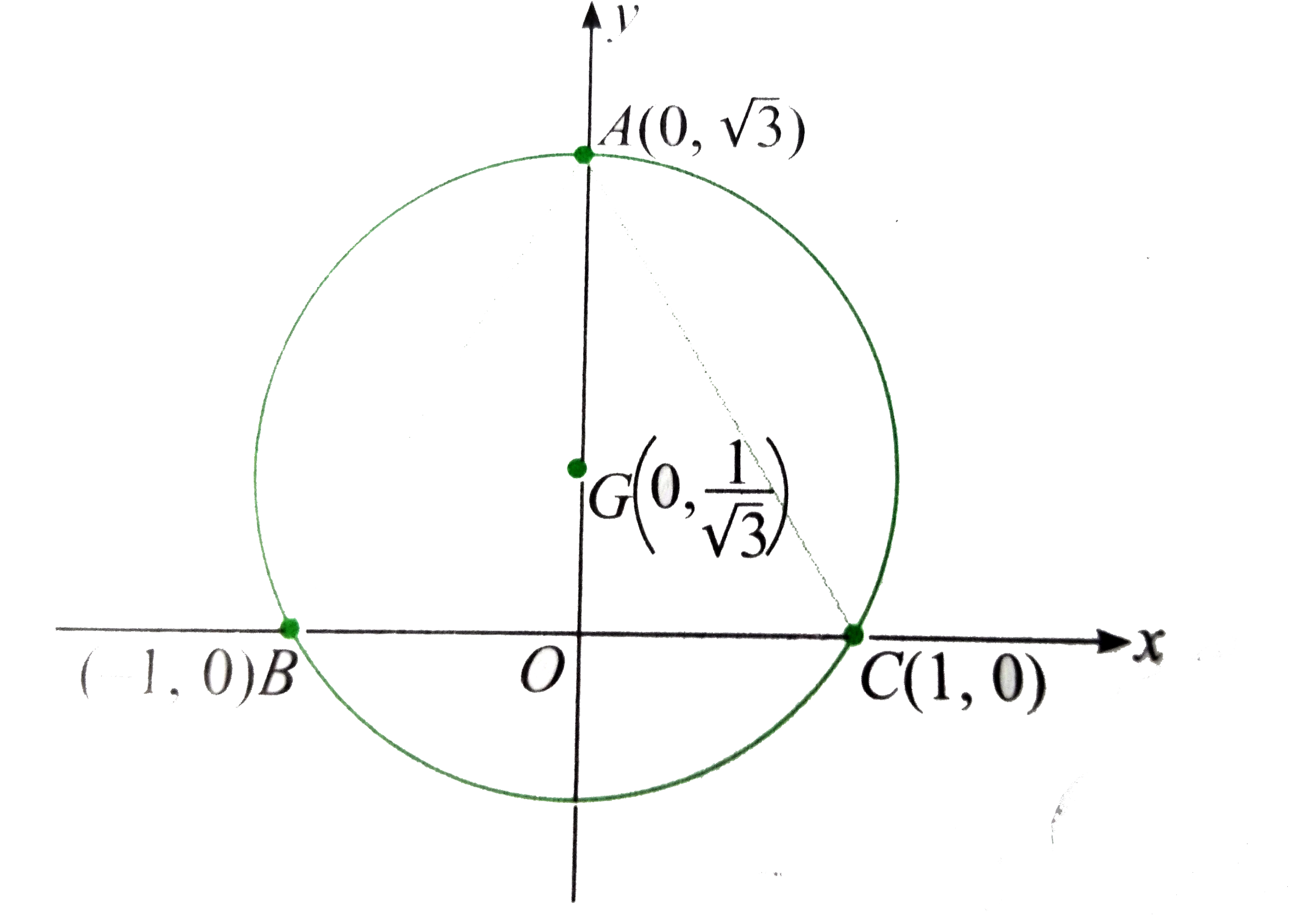
Let $B \equiv (- 1, 0), C \equiv (1, 0)$ .
Then A lies on y-axis.
$∴ O A = A B {sin 60}^{\circ} = \sqrt{3}$
$∴ A \equiv (0, \sqrt{3})$
In an equilateral triangle, circumcentre coincides with centroid.
Thus, circumcentre of triangle ABC is $G \equiv (\frac{- 1 + 1 + 0}{3}, \frac{\sqrt{3} + 0 + 0}{3}) \equiv (0, \frac{1}{\sqrt{3}})$
Circumradius $= A G = \sqrt{3} - \frac{1}{\sqrt{3}} = \frac{2}{\sqrt{3}}$
Therefore, equation of circumcircle of triangle ABC is ${(x - 0)}^{2} + {(y + \frac{1}{\sqrt{3}})}^{2} = {(\frac{2}{\sqrt{3}})}^{2}$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the centroid of an equilateral triangle is (1,1) and its one vertex is (2,-1) , then equation of the circumcircle of the triangle is
A $x (2) + y^{2} - 2 x - 2 y - 3 = 0$
B $x^{2} + y^{2} - 4 x + 2 y = 0$
C $x^{2} + y^{2} + 2 x + 2 y - 3 = 0$
D $x^{2} + y^{2} - 2 x + 2 y + 3 = 0$

CENGAGE ENGLISH-CIRCLE -MATRIX MATCH TYPE

Home
Ask Doubt
Profile