Question

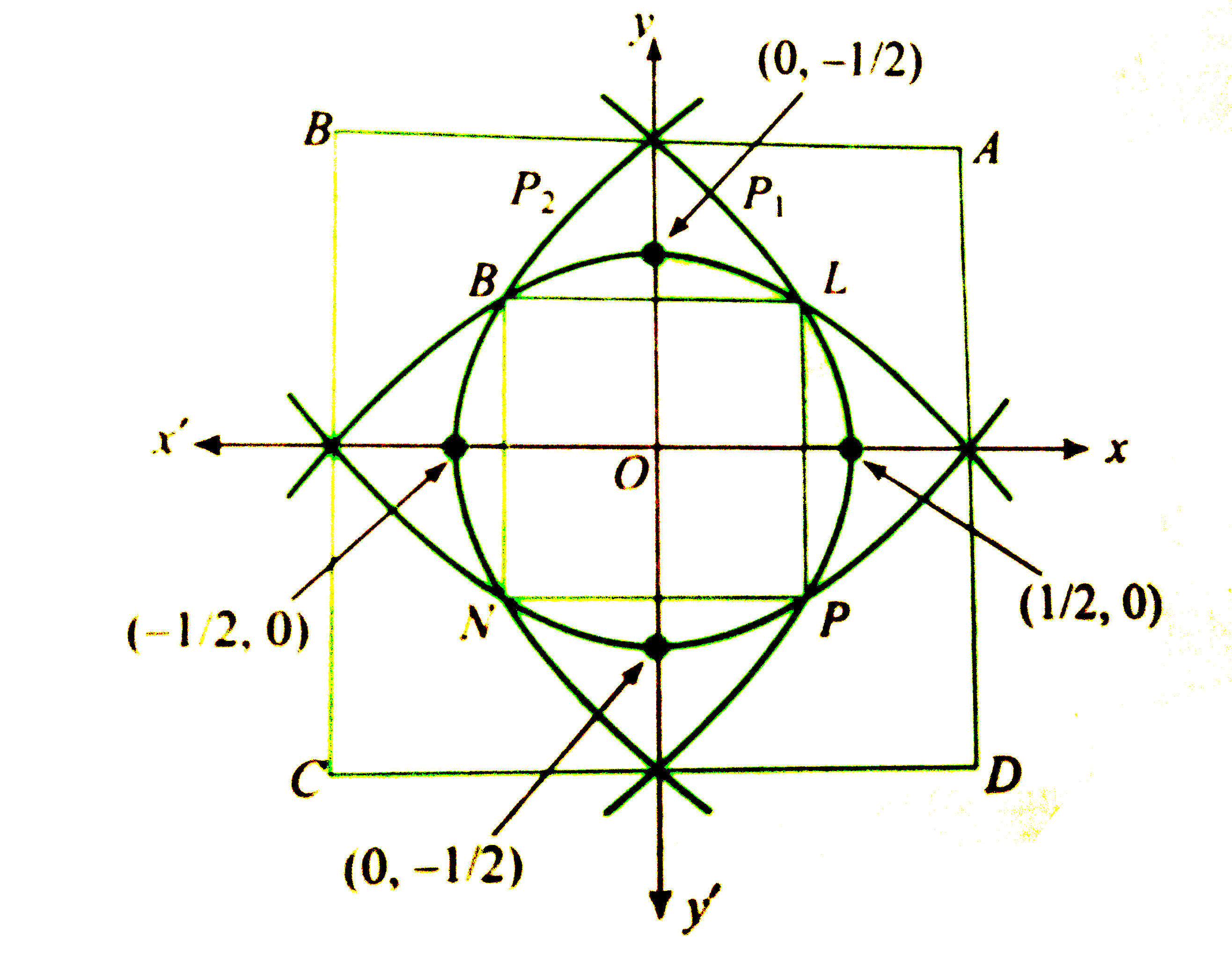
Consider a square with vertices at $(1,1),(-1,1),(-1,-1)\text{and}(1,-1)$. Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.

Explanation

Let us consider any point (x,y) inside the square such that its distance from origin is less than its distance from any of the edges. Consider edge AD. Therefore,
`OPltPM`
`rArr" "sqrt((x^(2)+y^(2)))lt1 -x or y^(2)lt-2(x-(1)/(2))" (1)"`
Above represents all points within the parabola `y^(2)=1-2x`.
If we consider the edge BC, then `OPltPN` will imply
`y^(2)lt2(x+(1)/(2))" (2)"`
Similarly, if we consider the edges AB and CD, we will have
`x^(2)lt-2(y-(1)/(2))" (3)"`
`x^(2)lt2(y+(1)/(2))" (4)"`
Hence, S consists of the region bounded by four parabolas meeting
`"the axes at "(pm(1)/(2),0)and (0,pm(1)/(2))`
The point L is intersection of `P_(1) and P_(3)` given by (1) and (3).

Solving, we get
`y^(2)-x^(2)=-2(x-y)=2(y-x)`
`"or "y-x=0`
`"or "y=x`
`rArr" "x^(2)+2x-1=0`
`"or "(x+1)^(2)=2`
`"or "x=sqrt(2)-1" as x is + ve"`
`therefore" L is "(sqrt(2)-1,sqrt(2)-1).`
`therefore" Total area = "4["Square of side "(sqrt(2)-1)+2int_(sqrt(2)-1)^(1//2)sqrt(1-sqrt(2x))dx]`
`=4{(sqrt(2)-1)^(2)+2int_(sqrt(2)-1)^(1//2)sqrt((1-2x))dx}`
`=4[3-2sqrt(2)-(2)/(3){(1-2x)^(3//2)}_(sqrt(2)-1)^(1//2)]`
`=4[3-2sqrt(2)-(2)/(3){0-(1-2sqrt(2)+2)^(3//2)}]`
`=4[3-2sqrt(2)+(2)/(3)(3-2sqrt(2))^(3//2)]`
`=4(3-2sqrt(2))[1+(2)/(3)sqrt((3-2sqrt(2)))]`
`=4(3-2sqrt(2))[1+(2)/(3)(sqrt(2)-1)]`
`=(4)/(3)(3-2sqrt(2))(1+2sqrt(2))=(4)/(3)[(4sqrt(2)-5)]`
`=(16sqrt(2)-20)/(3)` sq. units.