Plot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
Point P(x,y) lies in the first quadrant. Therefore, x,y>0
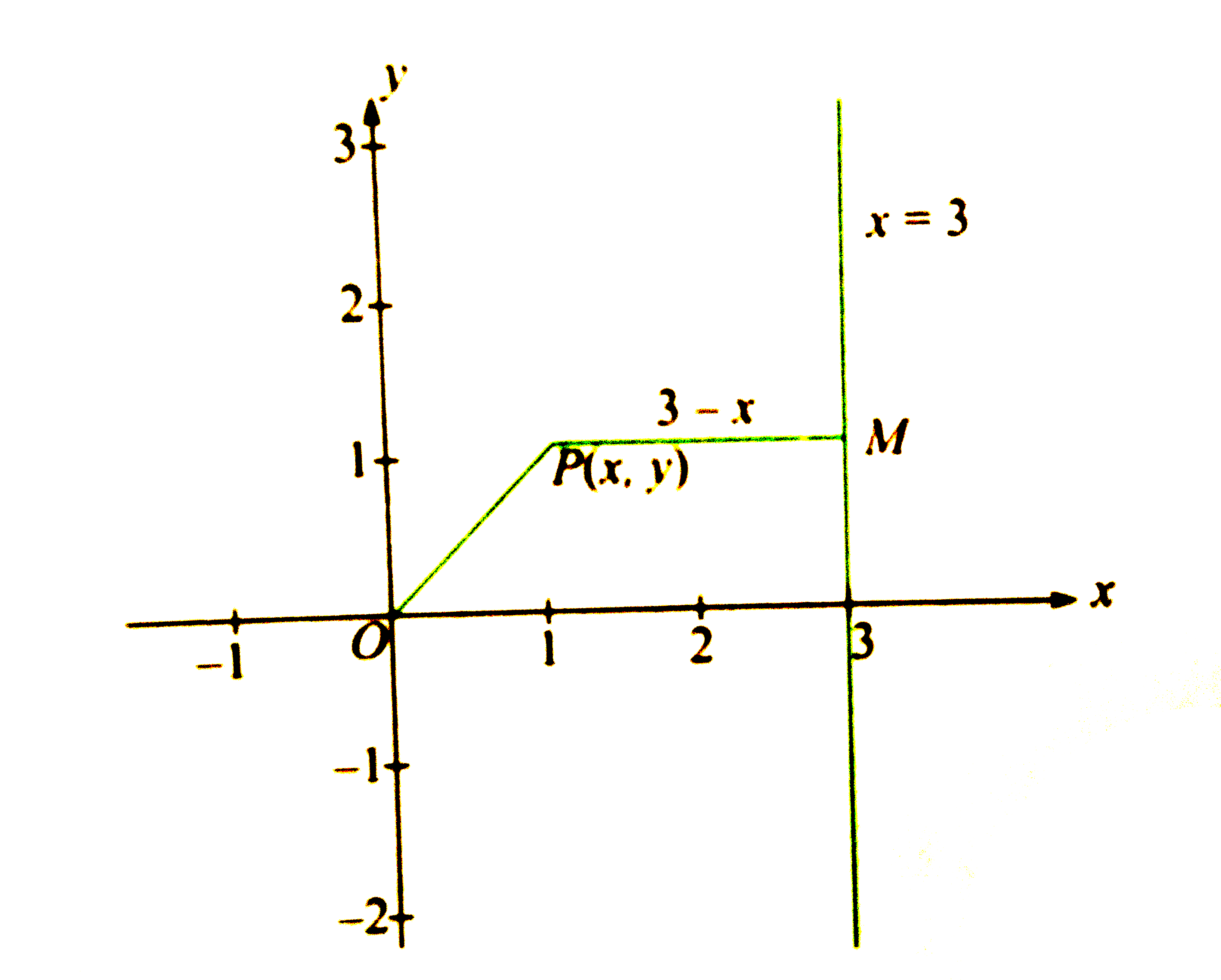
Also point P(x,y) is nearer to the origin than to the line x=3
Now OP=√x2+y2
Distance of P from line x-3=0 is PM =3-x
According to the question, OP<PM
⇒ √x2+y2<(3−x)
or x2+y2<x2−6x+9
or y2<−6x+9
or y2<−6(x−32)
Points satisfying above inequality lie inside parabola y2=9−6x in the first quadrant.
Parabola y2=−6(x−32) is concave to the left, having axis as
x-axis and vertex at (32,0) and directrix x=3
The required region as shown in the figure.

Area of the region =3∫09−y26dy=16(9y−y33)30
=16(27−9)=3 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Consider a square with vertices at (1,1)(−1,1)(−1,−1)and(1,−1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionConsider a square with vertices at (1,1),(−1,1),(−1,−1),and(1,−1). Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionConsider a square with vertices at (1,1),(−1,1),(−1,−1),and(1,−1). Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionIn which quadrant do the points lie: (4,3)
View SolutionFind the area of the region in the first quadrant enclosed by the y-axis, the line y=x and the circle x2+y2=32, using integration.
View SolutionFind the point on the straight line 2x+3y=6, which is closest to the origin.
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionFind the area of the region in the first quadrant enclosed by x-axis, the line y=√3 x and the circle x2+y2=16
View SolutionFind the area of the region in the first quadrant enclosed by the x-axis, the line y = x , and the circle x2+y2=32 .
View SolutionWhat is the number of square units in the area of the region in the first quadrant of the xy-plane that is bounded by y=|x|+2, the line x=5, the positive x-axis, ant the positive y-axis?
View Solution
