Find the area of the region R which is enclosed by the curve y≥√1−x2 and max {|x|,|y|}≤4.
For y≥√1−x2
points lie outside circle x2+y2=1 for y≥0and−1≤x≤1.
For max{|x|,|y|}≤4, where have
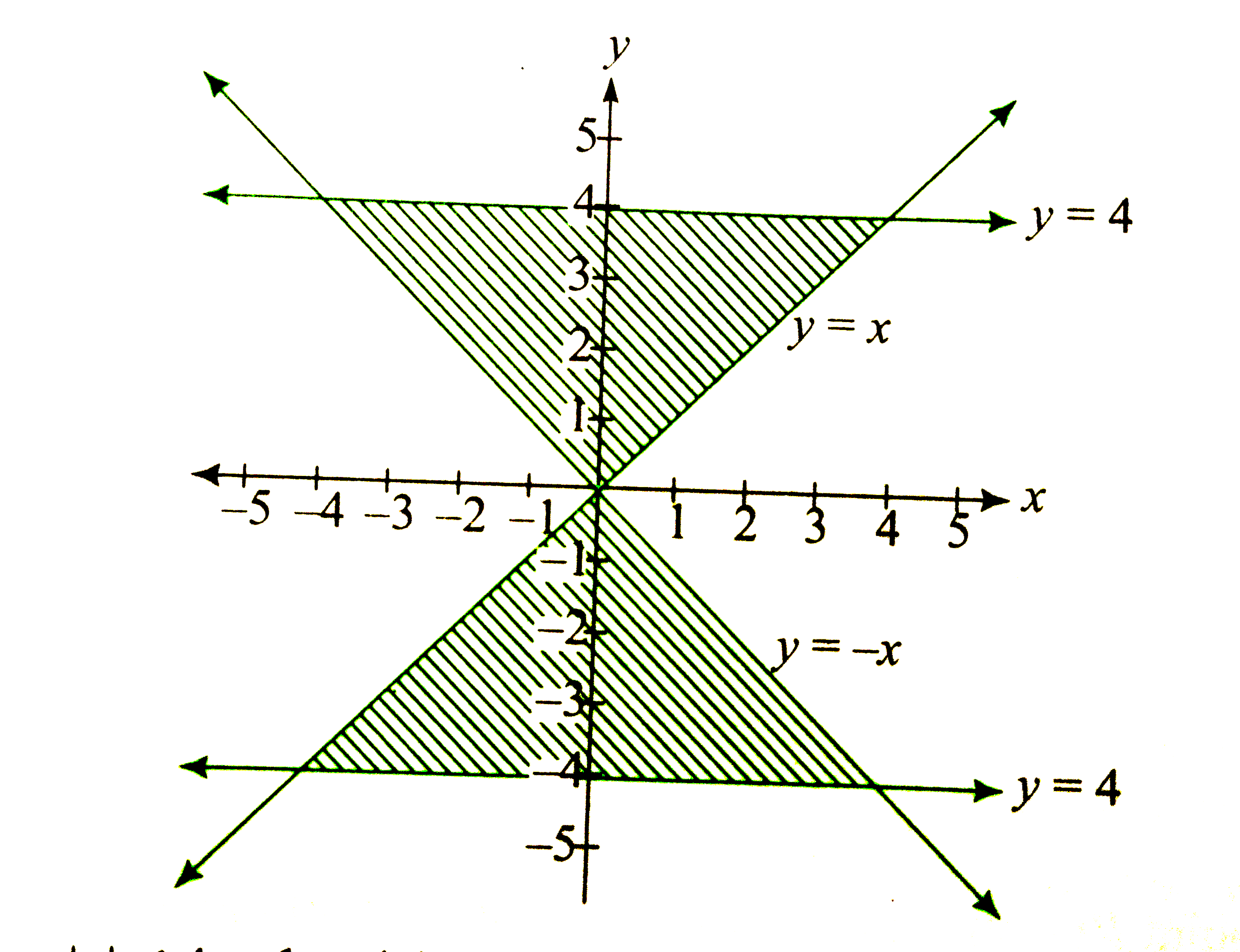
|y|≤4, when |x|<|y| (2)
The points satisfying above inequalities from region as shown in the figure.
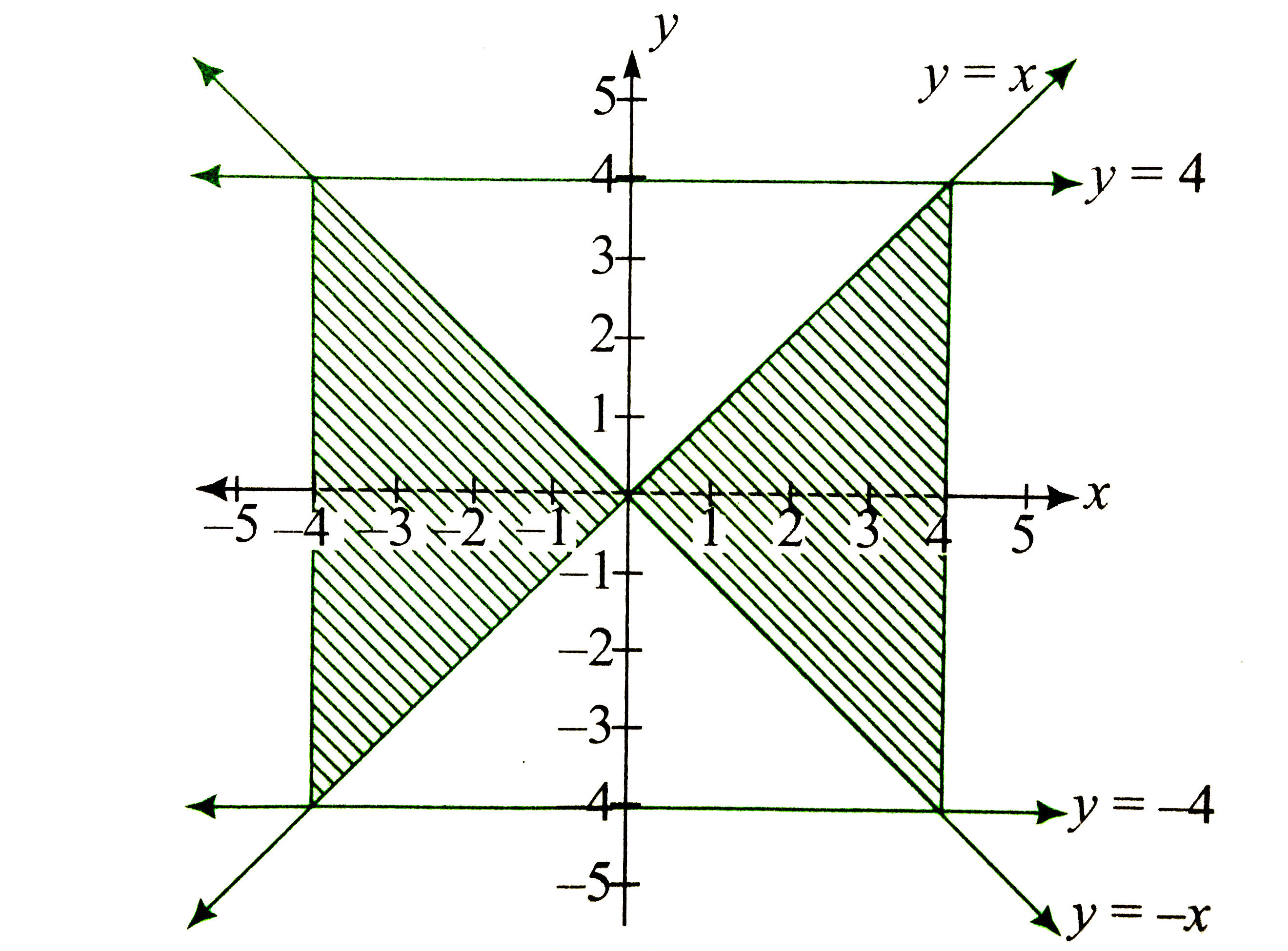
|x|≤4, when |y|<|x| (3)
The points satisfying above inequalities from region as shown in the figure.
The region (1)∩(2)∪(3)) is as shown in the figure.
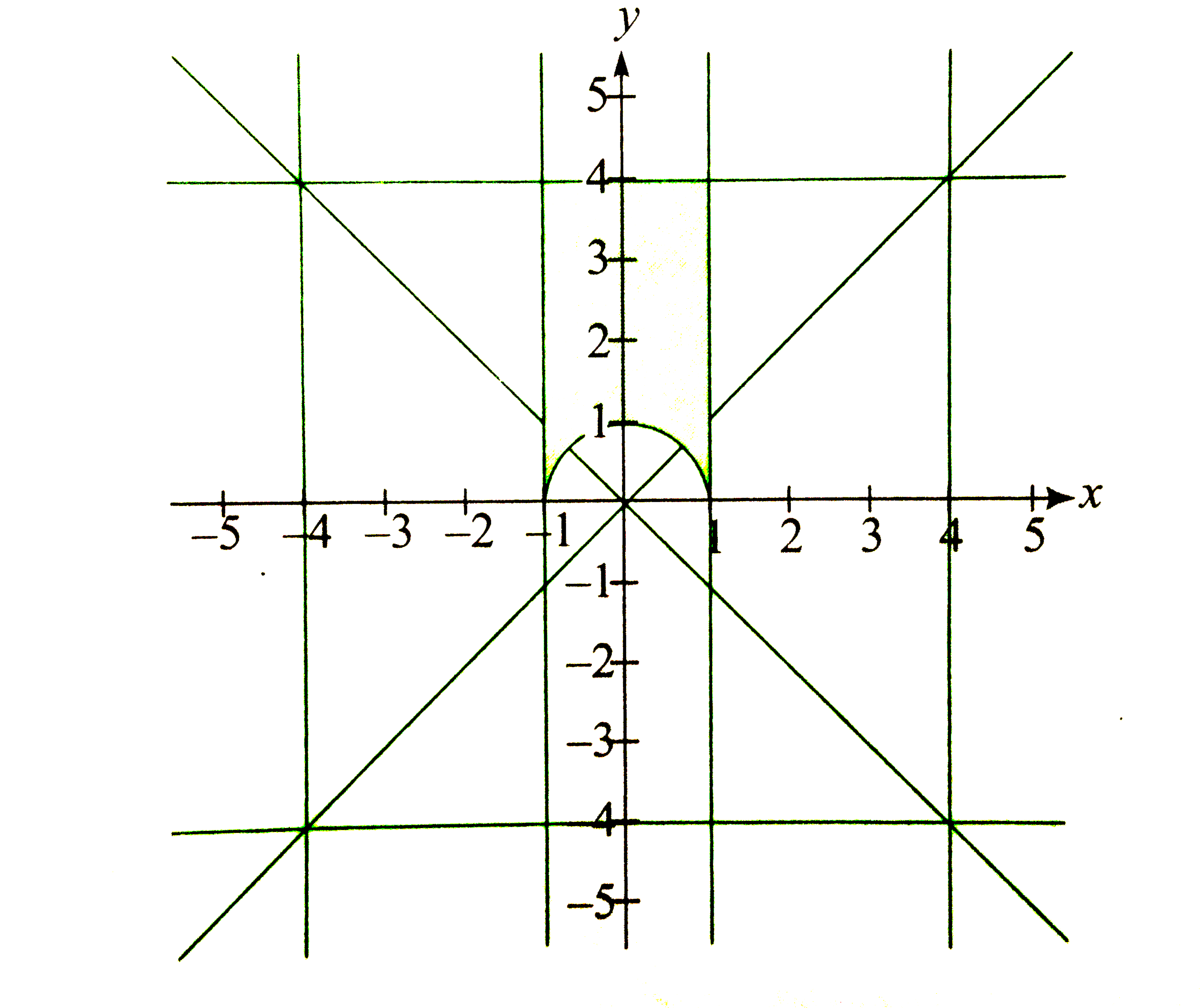
From the figure, required area is
=Area of rectangle- Area of semicircle having radius 1
=8−π2
Topper's Solved these Questions
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Solved Examples
Explore 10 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Concept Application Exercise 9.1
Explore 9 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Comprehension Type
Explore 5 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
Similar Questions
Find the area of the region enclosed by the curves
y=x2 and y = 2x
View SolutionFind the area of the region enclosed by the curves y=x2 and y=x3
View SolutionFind the area of the region enclosed by the given curves .
x=4−y2,x=0
View SolutionThe area of the region enclosed by the curve |y|=−(1−|x|)2+5, is
View SolutionFind the area of the region enclosed by the curves y=xlogx and y=2x−2x2.
View SolutionFind the area enclosed by the curve y=2x and max {|X|, |y|} = 1
View SolutionFind the area of the region enclosed by the curves
y=x2−4x+3 and the x-axis
View SolutionFind the area of the region enclosed by the curve y=∣∣∣x−1x∣∣∣(x>0) and the line y=2
View SolutionFind the area of the region enclosed by the given curves .
y=cosx,y=1−2xπ
View SolutionFind the area of the region enclosed by the given curves .
y=x3+3,y=0,x=−1,x=2
View Solution