Find the area of the figure bounded by the parabolas x=−2y2,x=1−3y2.
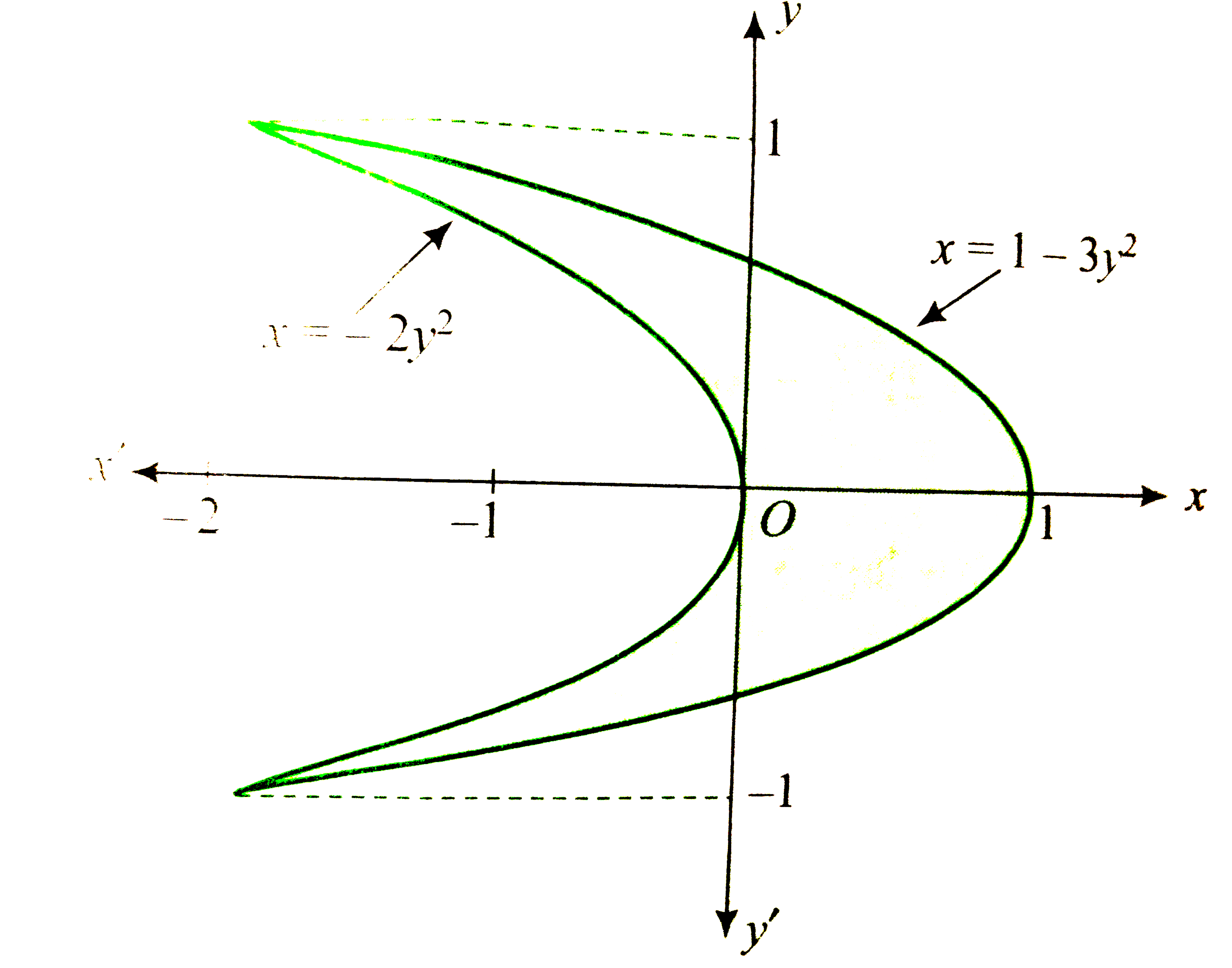
Solving the equation x=−2y2,x=1−3y2, we find the ordinates of the point of intersection of the two curves are
y1=−1,y2=1. The points are (−2,1)and(−2,1).
The required area is given by (Integrating along y-axis)
A=2∫10(x1−x2)dy
=2∫[(1−3y2)−(−2y2)]dy
=2∫10(1−y2)dy
=2[y−y33]10=43
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area of the region bounded by the parabolas x=−2y2 and x=1−3y2 is
View SolutionFind the area of the region bounded by the parabola y=x2 and y=|x| .
View SolutionFind the area of the region bounded by the parabola y=x2 and y=|x|.
View SolutionFind the area of the region bounded by the two parabolas y=x2and y2=x.
View SolutionUsing integration calculate the area of the region bounded by the two parabolas y=x2 and x=y2
View SolutionFind the area of the figure bounded by parabola y=−x2−2x+3, the tangent to it at the point (2−5) and the y-axis.
View SolutionFind the area of the region bounded by the parabola x2=4y\ and the line x=4y−2
View SolutionFind the area of the region bounded by the parabola y2=2x and straight line x−y=4.
View SolutionFind the area of the region bounded by the parabola y2=4ax, its axis and two ordinates x=a and x=2a.
View SolutionFind the area of the region bounded by the parabola y2=2pxandx2=2py.
View Solution
