Doubtnut Promotions Sticky

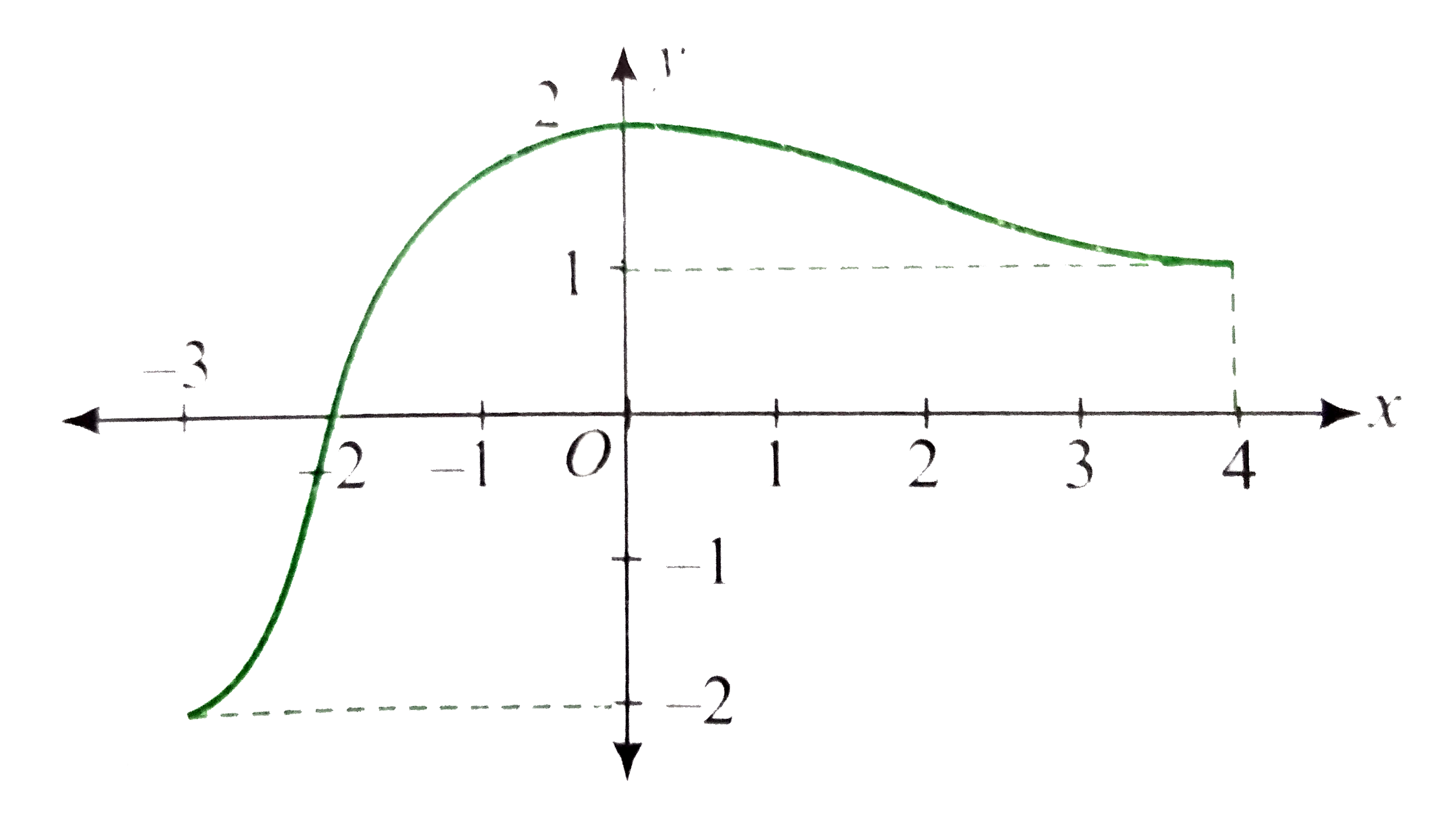
Consider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
Consider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph. If h(x)=|f(x)-(3)/(2)| has range [e, f] and n be number of real solutions of h(x)=(1)/(4),
If h(x)=∣∣∣f(x)−32∣∣∣ has range [e, f] and n be number of real solutions of h(x)=14, then (n+e+2f) is

A

8

B

9

C

10

D

11

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

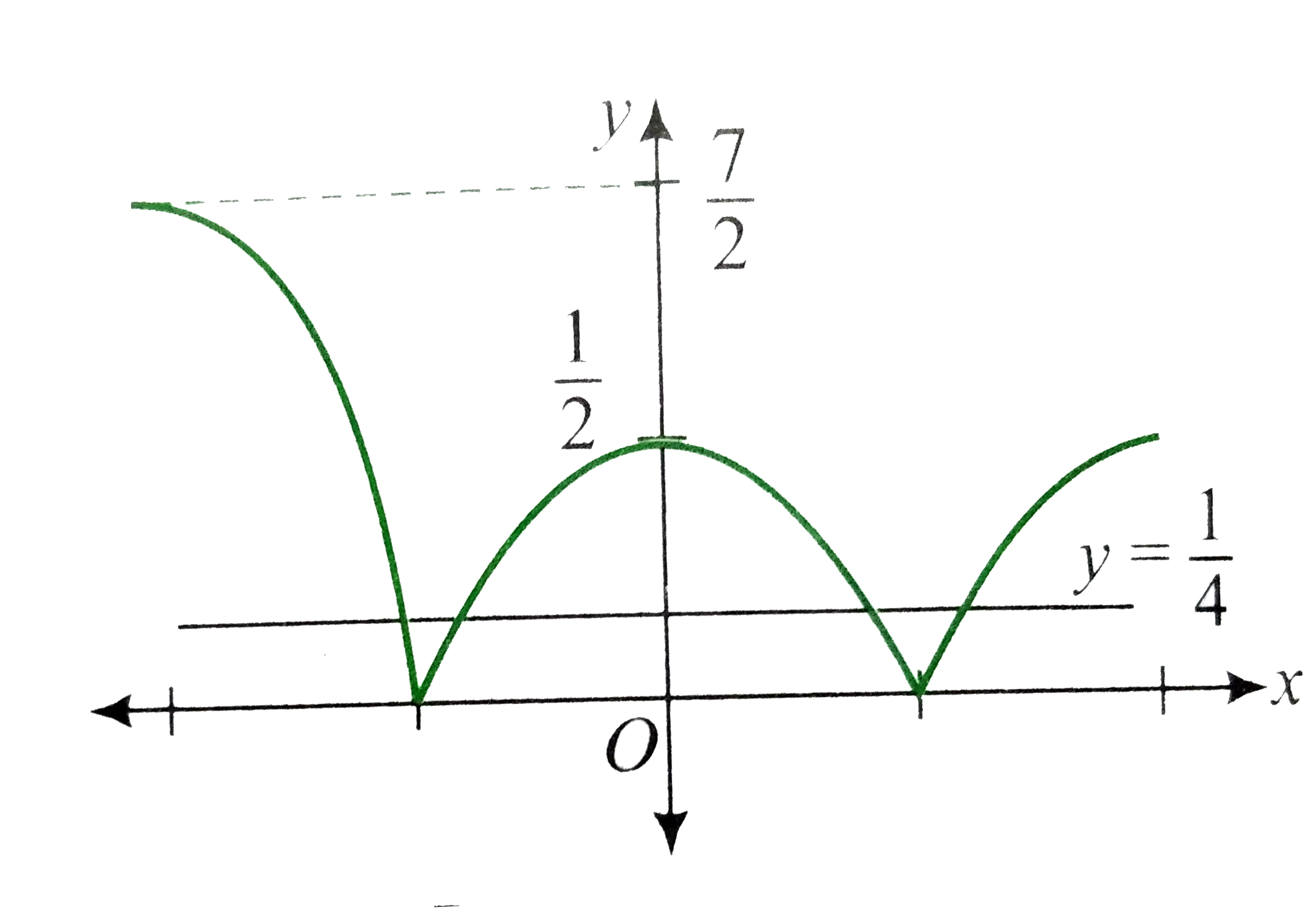
ocr_image
Range of h(x)=[0,72]
Number of solutions of h(x)=14 is n=4.
∴(n+e+2f)=4+0+7=11.

|
Updated on:21/07/2023
Class 12MATHSRELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The domain and range of the real function f defined by f(x)=14x2−1 are

    ADomain ={−12,12}, Range =−{−∞,−1)∪(0,∞)
    BDomain R={−12,12}, Range =−{−∞,−1)∪(0,∞)
    CDomain =[−12,12], Range =−{−∞,−1)∪(0,∞)
    DDomain =R−[−12,12], Range =−{−∞,−1)∪(2,∞)