Draw the graph and find the points of discontinuity for f(x)=[x2−x−1],x∈[−1,2] ([.] represents the greatest integer function).
f(x)=[x2−x−1],x∈[−1,2]
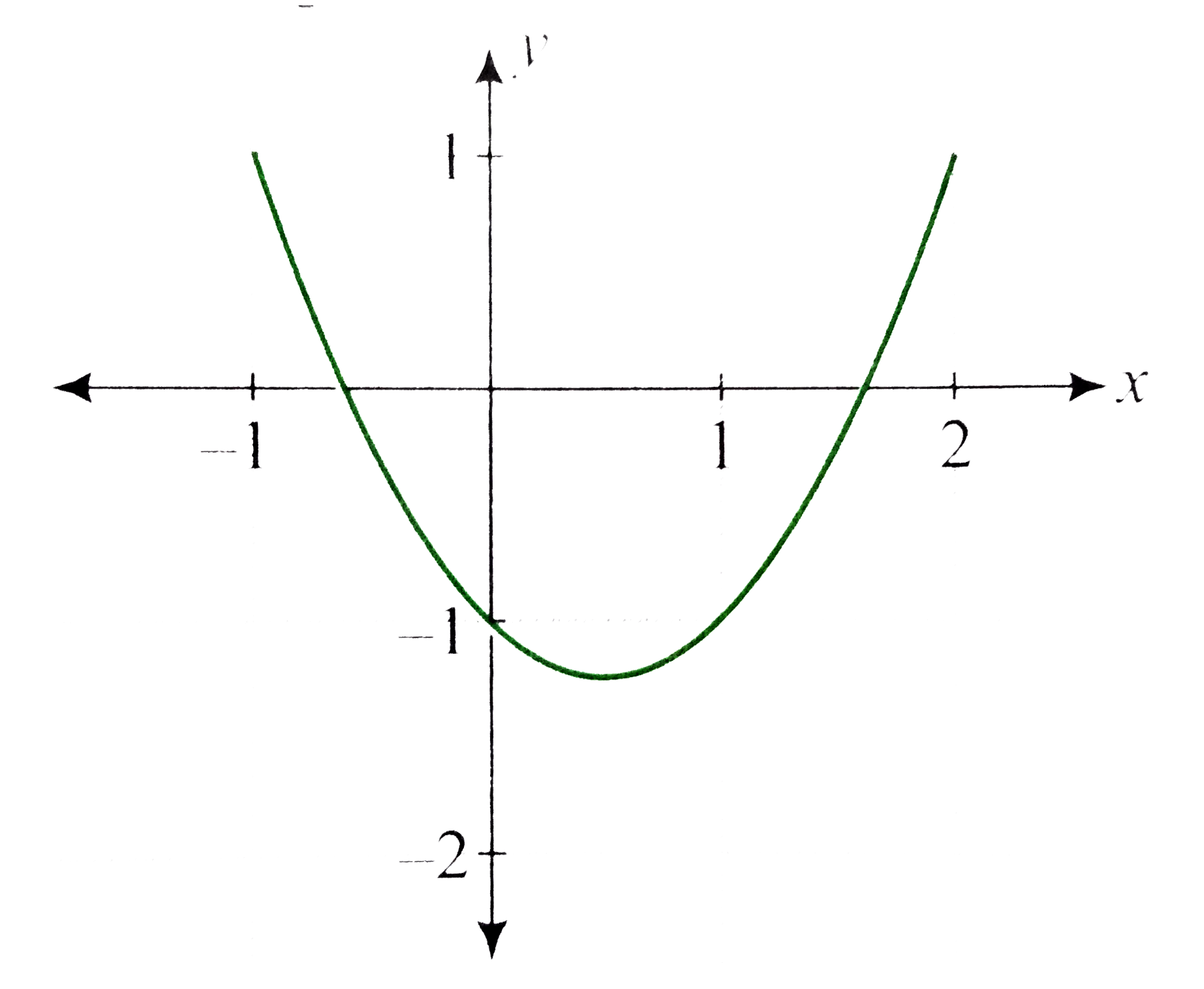
Let us first draw the graph of y=x2−x−1, which is upward parabola having vertex at (1/2,−5/4)
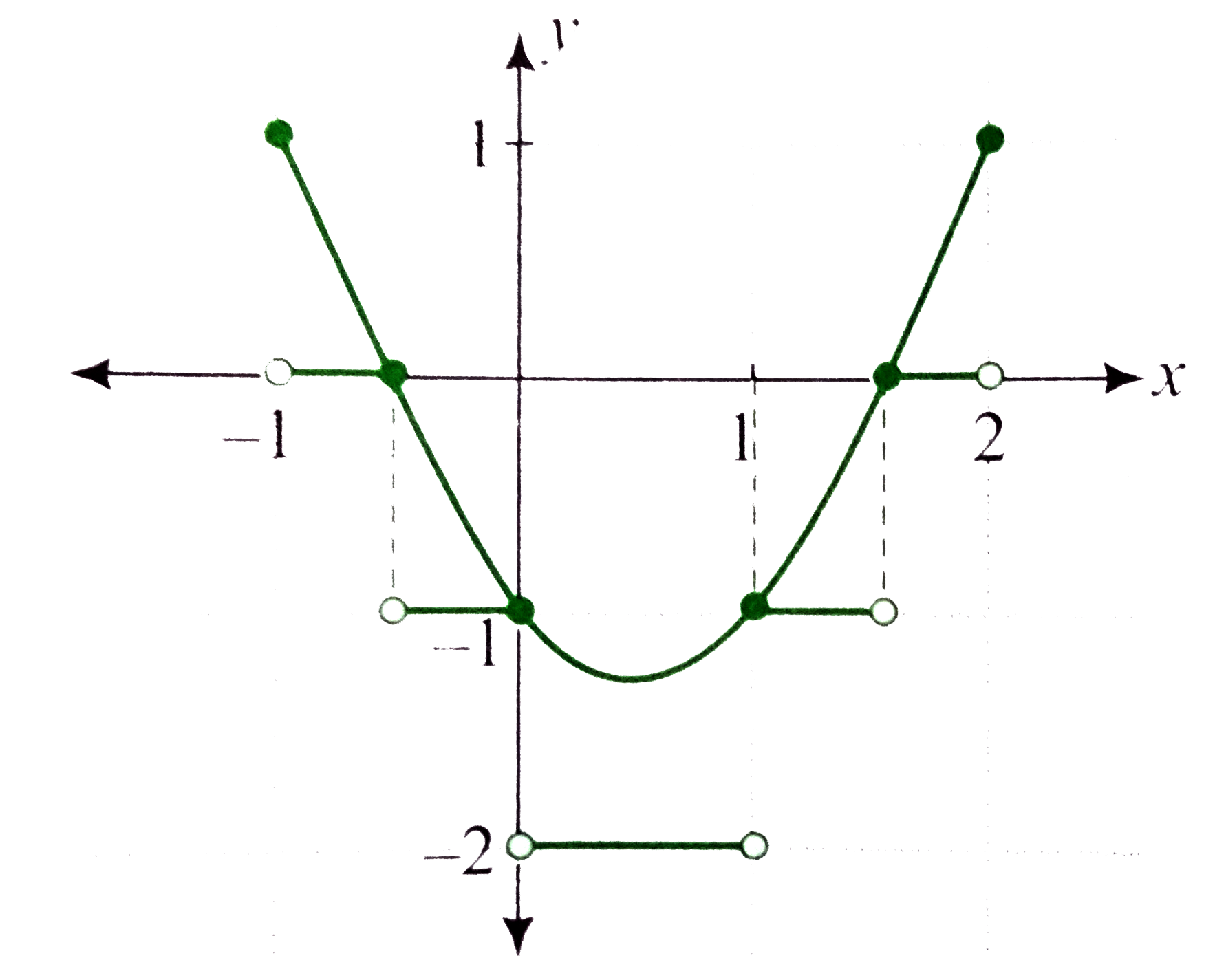
The graph of f(x)=[x2−x−1] can be drawn as shown in the following figure.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Single Correct Answer Type
125 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Multiple Correct Answer Type
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.14
13 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Draw the graph and find the points of discontinuity f(x)=[2cosx] , x∈[0,2π] . ([.] represents the greatest integer function.)
View SolutionDraw the graph and find the points of discontinuity f(x)=[2cosx] , x∈[0,2π] . ([.] represents the greatest integer function.)
View SolutionDraw the graph and find the points of discontinuity f(x)=[2cosx] , x∈[0,2π] . ([.] represents the greatest integer function.)
View SolutionFind the number of points of discontinuity for f(x)=[6sinx],0≤π([.] represents the greatest integer function).
View SolutionFind the points of discontinuity of the function: f(x)=[[x]]−[x−1],where[.] represents the greatest integer function
View SolutionDraw the graph and discuss the continuity of f(x)=[sinx+cosx],x∈[0,2π), where [.] represents the greatest integer function.
View SolutionDraw the graph and discuss the continuity of f(x)=[sinx+cosx],x∈[0,2π), where [.] represents the greatest integer function.
View SolutionFind the domain of the function f(x)=1[x]2−7[x]−8, where [.] represents the greatest integer function.
View SolutionIf f(x)=|x−1|.([x]=[−x]), then (where [.] represents greatest integer function)
View SolutionDraw the graph of y=[4−x2],|x|≤2, where [.] represents the greatest integer function.
View Solution