Question

Solve (a) $\tan x<2$

$\cos x\le -\frac{1}{2}$

Answer

(a) `underset(n in Z)(cup)(npi-(pi)/(2),n pi+tan^(-1)2)`
(b) `underset (n in Z)(cup)[2npi+(2pi)/(3),2n pi+(4pi)/(3)]`

Explanation

(a) We know that `tanx ` is periodic with period `pi.` So, check the solution in the interval `(-(pi)/(2),(pi)/(2)).`

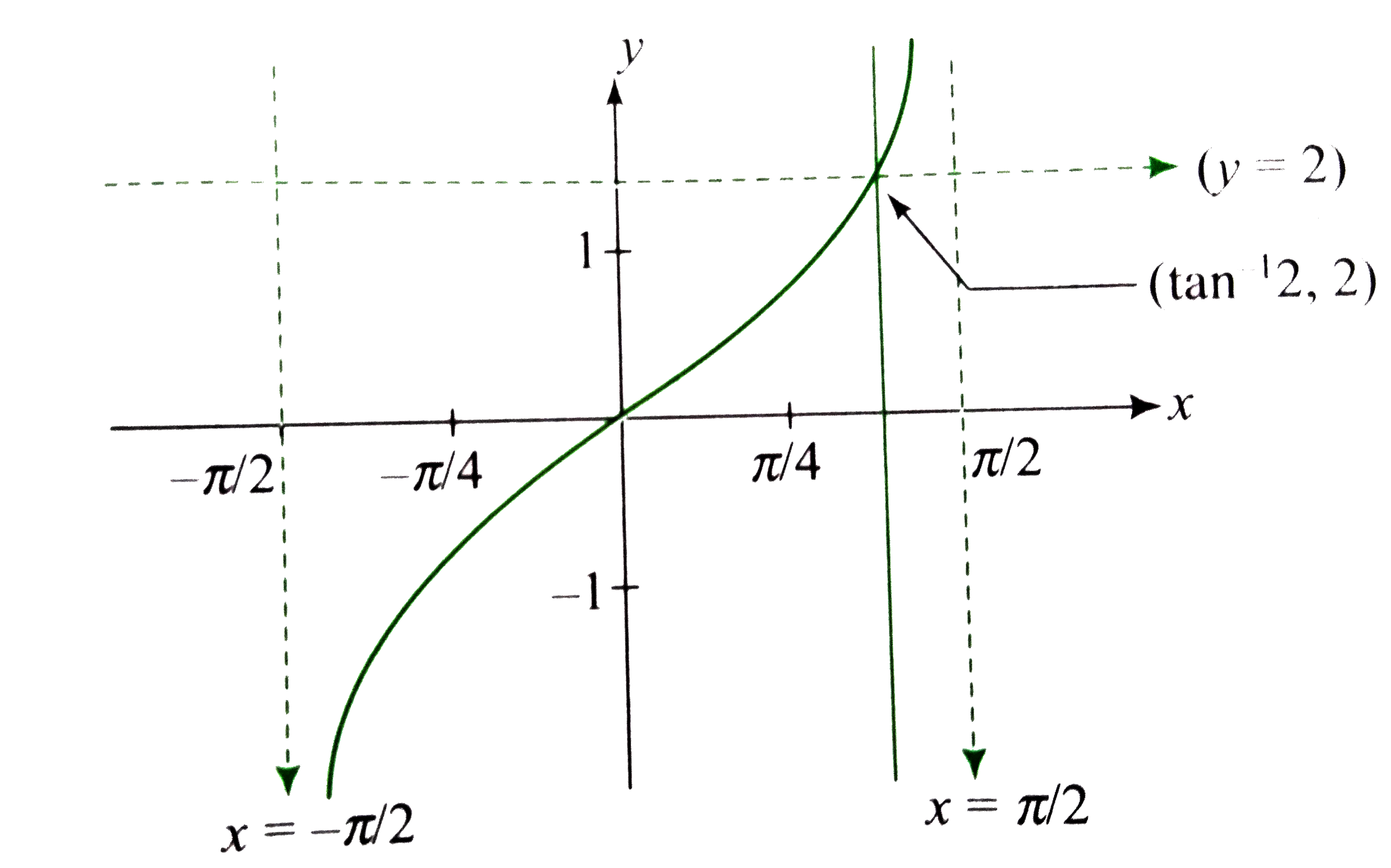
It is clear from the figure that `tanx lt 2` when
`-(pi)/(2) lt x lt tan^(-1)2.`
Therefore, general solution is
`underset(n in Z)(cup)(npi-(pi)/(2),n pi+tan^(-1)2)`
(b) `cosx` is periodic with period `2pi`.
So, check the solution in `[0,2pi].`

It is clear from the figure that `cos x le -(1)/(2)` when
`(2pi)/(3) le x le (4pi)/(3).`
On generalizing the above solution, we get
`x inunderset (n in Z)(cup)[2npi+(2pi)/(3),2n pi+(4pi)/(3)]`