img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_ALG_DPP_4_2_E01_231_Q01.png" width="80%"gt
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
Ifα=13, then the least value of n for which An>110 is
4
5
6
7
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a unit square ABCD with each side divided in the ratio α:(1−α). We need to find the least value of n such that the area An of the nth square is greater than 110.
Step 2: Define Variables
Let:
- An = Area of the nth square
- an = Side length of the nth square
Since the area of a square is given by the square of its side length, we have:
An=a2n
Step 3: Establish the Relationship Between Squares
From the problem, we know that the side length of the new square can be expressed in terms of the previous square's side length. The relationship is given by:
a2n+1=(1−α)2+α2a2n
Substituting An into the equation gives:
An+1=(1−α)2+α2An
Step 4: Substitute α=13
Now, substituting α=13:
An+1=(1−13)2+(13)2An
Calculating the terms:
An+1=(23)2+(13)2An=49+19An
Step 5: Express in Terms of An
Rearranging gives:
An+1=49+19An
Step 6: Find the Recurrence Relation
We can rewrite the recurrence relation as:
An+1=19An+49
Step 7: Initial Condition
Since the area of the first square A1=1 (as it is a unit square):
A1=1
Step 8: Calculate Subsequent Areas
Using the recurrence relation:
- For n=1:
A2=19⋅1+49=59
- For n=2:
A3=19⋅59+49=581+3681=4181
- For n=3:
A4=19⋅4181+49=41729+324729=365729
- For n=4:
A5=19⋅365729+49=3656561+29166561=32816561
Step 9: Check When An>110
We need to find the smallest n such that:
An>110
Calculating the values:
- A1=1>110
- A2=59≈0.555>110
- A3=4181≈0.506>110
- A4=365729≈0.500>110
- A5=32816561≈0.500>110
Conclusion
The least value of n for which An>110 is n=1.
We have a unit square ABCD with each side divided in the ratio α:(1−α). We need to find the least value of n such that the area An of the nth square is greater than 110.
Let:
- An = Area of the nth square
- an = Side length of the nth square
An=a2n
From the problem, we know that the side length of the new square can be expressed in terms of the previous square's side length. The relationship is given by:
a2n+1=(1−α)2+α2a2n
Substituting An into the equation gives:
An+1=(1−α)2+α2An
Now, substituting α=13:
An+1=(1−13)2+(13)2An
Calculating the terms:
An+1=(23)2+(13)2An=49+19An
Rearranging gives:
An+1=49+19An
We can rewrite the recurrence relation as:
An+1=19An+49
Since the area of the first square A1=1 (as it is a unit square):
A1=1
Using the recurrence relation:
- For n=1:
A2=19⋅1+49=59
- For n=2:
A3=19⋅59+49=581+3681=4181
- For n=3:
A4=19⋅4181+49=41729+324729=365729
- For n=4:
A5=19⋅365729+49=3656561+29166561=32816561
We need to find the smallest n such that:
An>110
- A1=1>110
- A2=59≈0.555>110
- A3=4181≈0.506>110
- A4=365729≈0.500>110
- A5=32816561≈0.500>110
The least value of n for which An>110 is n=1.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - Multiple Correct Answer4videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ILLUSTRATION 5.11videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
PROBABILITY II
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
Similar Questions
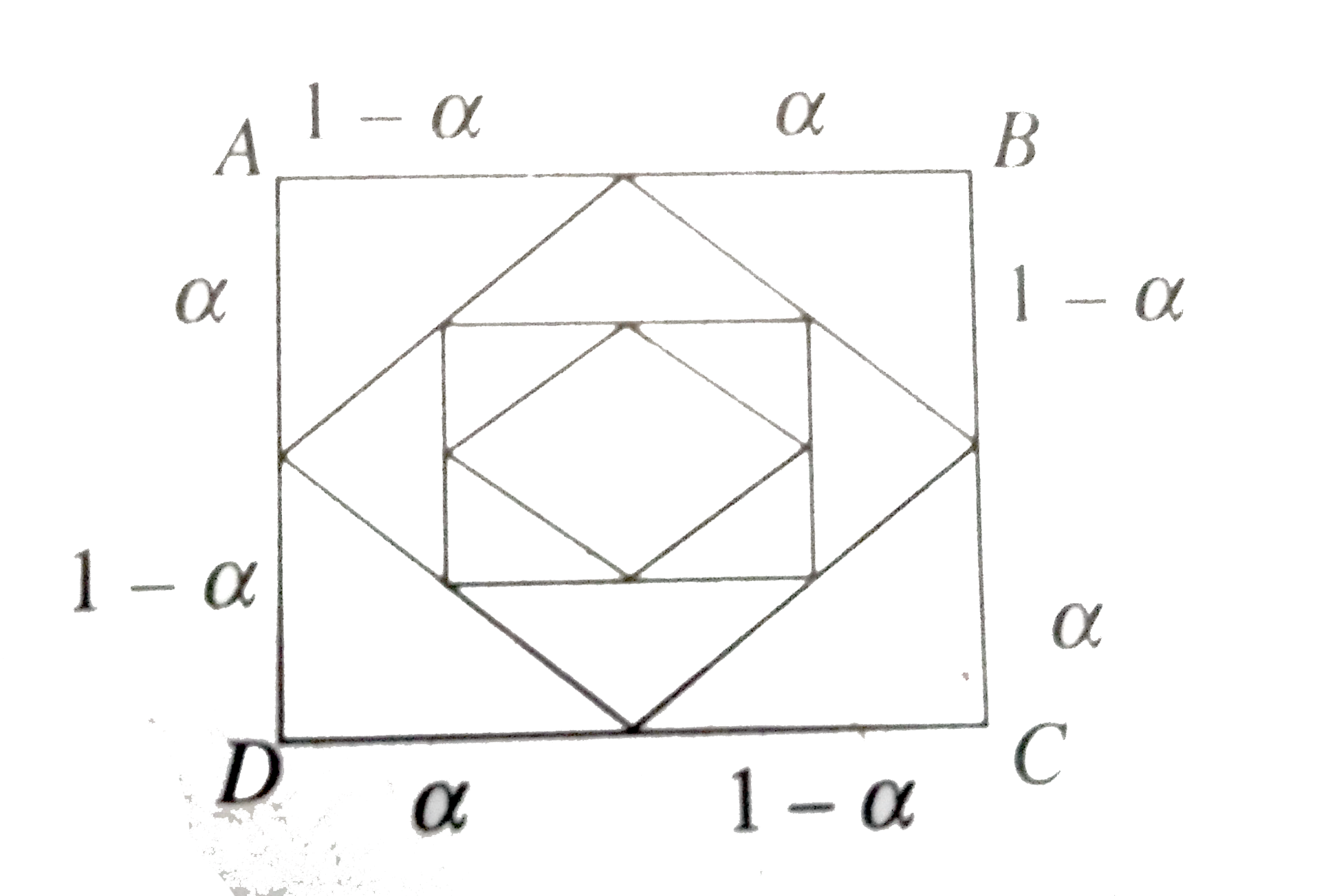
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which ∞∑n=1An=83 is/areView Solution Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which side of nth square equal to the diagonal of (n+1)th square isView SolutionIdentify A,B,C and D,E
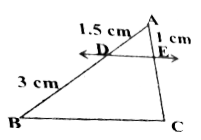
View SolutionIn the given fig. If DE||BC Find EC.
 View Solution
View SolutionAt point P, the value of dydx is :
 View Solution
View SolutionThe side of a given square is equal to a. The mid-points of its sides are joined to form a new square. Again, the mid-points of the sides of this new square are joined to form another square. This process is continued indefinitely. Find the sum of the areas of the squares and the sum of the perimeters of the squares.
View SolutionThe equation of straight line shown in figure is :
 View Solution
View SolutionThe sides of the triangle are sinα , cosα and √1+sinαcosα for some 0<α<π2. Then the greatest angle of the triangle is
View SolutionWhat is the distance OA for the square shown in figure :-
 View Solution
View SolutionA square is drawn by joining mid pint of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued in definitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
View Solution
