If a3−3a2+5a−17=0 and b3−3b2+5b+11=0 are such that a+b is a real number, then the value of a+b is
−1
1
2
−2
The correct Answer is:C
To solve the equations a3−3a2+5a−17=0 and b3−3b2+5b+11=0 under the condition that a+b is a real number, we can follow these steps:
Step 1: Define a+b
Let a+b=λ. Then we can express b in terms of a:
b=λ−a
Step 2: Substitute b into the second equation
Now, substitute b=λ−a into the second equation:
(λ−a)3−3(λ−a)2+5(λ−a)+11=0
Step 3: Expand the equation
Expanding (λ−a)3:
(λ−a)3=λ3−3λ2a+3λa2−a3
Expanding −3(λ−a)2:
−3(λ−a)2=−3(λ2−2λa+a2)=−3λ2+6λa−3a2
Expanding 5(λ−a):
5(λ−a)=5λ−5a
Step 4: Combine all terms
Now, combine all the terms:
λ3−3λ2+5λ+11−a3+3λ2a−3a2+6λa−5a=0
This simplifies to:
λ3−a3+(3λ2−3)a2+(6λ−5)a+(λ3+5λ+11)=0
Step 5: Rearranging the equation
Rearranging gives:
−a3+(3λ2−3)a2+(6λ−5)a+(λ3+5λ+11)=0
Step 6: Compare coefficients
Now, we compare this equation with the first equation a3−3a2+5a−17=0. This gives us:
1. Coefficient of a3: −1 matches −1
2. Coefficient of a2: 3λ2−3=−3 implies 3λ2=0 so λ2=0 which gives λ=0
3. Coefficient of a: 6λ−5=5 implies 6λ=10 which is consistent with λ=2
4. Constant term: λ3+5λ+11=−17 implies 23+5(2)+11=8+10+11=29 which does not satisfy.
Step 7: Solve for λ
From the coefficients, we find that λ=2 satisfies the equations.
Final Answer
Thus, the value of a+b is:
2
Let a+b=λ. Then we can express b in terms of a:
b=λ−a
Now, substitute b=λ−a into the second equation:
(λ−a)3−3(λ−a)2+5(λ−a)+11=0
Expanding (λ−a)3:
(λ−a)3=λ3−3λ2a+3λa2−a3
Expanding −3(λ−a)2:
−3(λ−a)2=−3(λ2−2λa+a2)=−3λ2+6λa−3a2
Expanding 5(λ−a):
5(λ−a)=5λ−5a
Now, combine all the terms:
λ3−3λ2+5λ+11−a3+3λ2a−3a2+6λa−5a=0
This simplifies to:
λ3−a3+(3λ2−3)a2+(6λ−5)a+(λ3+5λ+11)=0
Rearranging gives:
−a3+(3λ2−3)a2+(6λ−5)a+(λ3+5λ+11)=0
Now, we compare this equation with the first equation a3−3a2+5a−17=0. This gives us:
1. Coefficient of a3: −1 matches −1
2. Coefficient of a2: 3λ2−3=−3 implies 3λ2=0 so λ2=0 which gives λ=0
3. Coefficient of a: 6λ−5=5 implies 6λ=10 which is consistent with λ=2
4. Constant term: λ3+5λ+11=−17 implies 23+5(2)+11=8+10+11=29 which does not satisfy.
From the coefficients, we find that λ=2 satisfies the equations.
Thus, the value of a+b is:
2
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Comprehension
12 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer
6 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Knowledge Check
If 5a=6b+7anda−b=3, what is the value of b2 ?
A2B4C5.5D11If 5b=6a+16and9b=7b−20, then what is the value of 3a−2b?
A−8B−4C4D8
If 2x3+ax2+bx+4=0 (a and b are positive real numbers) has three real roots.
The minimum value of (a+b)3 is
View SolutionIf 2x3+ax2+bx+4=0 (a and b are positive real numbers) has three real roots.
The minimum value of b3 is a. 108 b. 216 c. 432 d. 864
View Solutionif 3a−c=5band3a+3b−c=40, what is the value of b?
View SolutionIf a:b=2:5, . find the value of 3a+2b4a+b
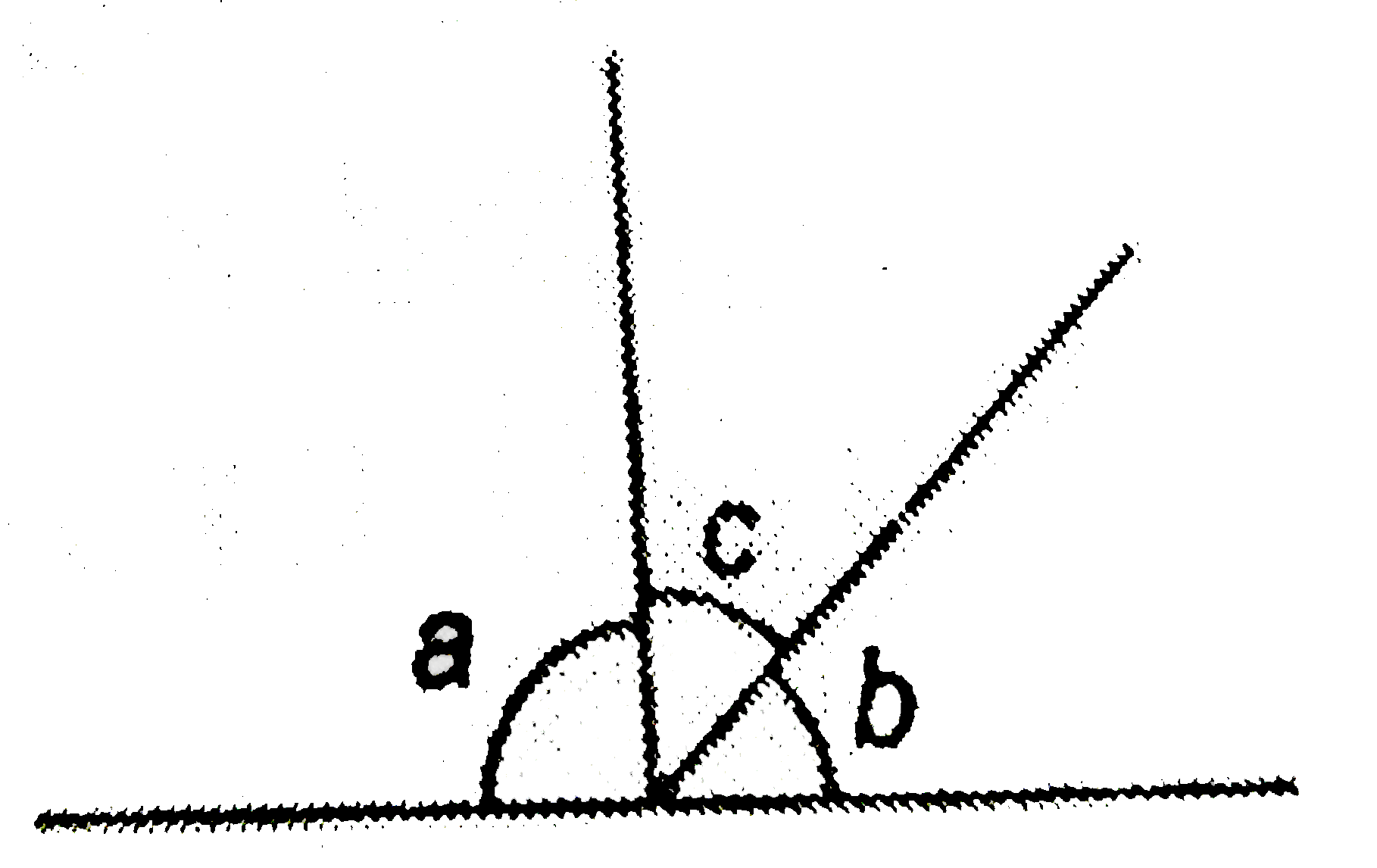
View SolutionIn the given figure if c=3b and a=5b find the value of a and b
View SolutionIf a≠banda2=5a−3,b2=5b−3, then form that equation whose roots are abandba.
View Solution
