ABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
(p2+q2sinθpcosθ+qsinθ
(p2+q2)cosθpcosθ+qsinthet
p2+q2p2cosθ+q2sinθ
(p2+q2)sinθ(pcosθ+qsinθ)
The correct Answer is:A
To solve the problem, we need to find the length of side AB in trapezium ABCD, given that AB is parallel to CD, BC is perpendicular to CD, and we have the angles and lengths defined.
1. Understanding the Trapezium:
- We have trapezium ABCD where AB || CD.
- BC is perpendicular to CD, which means angle BCD = 90°.
2. Identifying Angles:
- Given angle ADB = θ.
- Let angle CDB = α. Since AB || CD, angle CDB = angle ADB = α.
3. Using Right Triangle Properties:
- In triangle BCD, we can apply the Pythagorean theorem:
DB=√BC2+CD2=√p2+q2
- Here, BC = p and CD = q.
4. Finding Cosine and Sine of Angle α:
- From triangle CDB:
- Cosine of angle α:
cosα=CDDB=q√p2+q2
- Sine of angle α:
sinα=BCDB=p√p2+q2
5. Applying the Sine Rule in Triangle ADB:
- According to the sine rule:
ABsinθ=DBsin(π−θ−α)
- Since sin(π−x)=sinx, we have:
ABsinθ=√p2+q2sin(θ+α)
6. Expanding sin(θ+α):
- Using the sine addition formula:
sin(θ+α)=sinθcosα+cosθsinα
- Substitute the values of cosα and sinα:
sin(θ+α)=sinθ(q√p2+q2)+cosθ(p√p2+q2)
7. Substituting Back:
- Now substituting this back into the sine rule equation:
AB=√p2+q2⋅sinθsinθ⋅q√p2+q2+cosθ⋅p√p2+q2
- Simplifying gives:
AB=(p2+q2)⋅sinθq⋅sinθ+p⋅cosθ
Final Answer:
Thus, the length of AB is given by:
AB=p2+q2⋅sinθp⋅cosθ+q⋅sinθ
- We have trapezium ABCD where AB || CD.
- BC is perpendicular to CD, which means angle BCD = 90°.
- Given angle ADB = θ.
- Let angle CDB = α. Since AB || CD, angle CDB = angle ADB = α.
- In triangle BCD, we can apply the Pythagorean theorem:
DB=√BC2+CD2=√p2+q2
- Here, BC = p and CD = q.
- From triangle CDB:
- Cosine of angle α:
cosα=CDDB=q√p2+q2
- Sine of angle α:
sinα=BCDB=p√p2+q2
- According to the sine rule:
ABsinθ=DBsin(π−θ−α)
- Since sin(π−x)=sinx, we have:
ABsinθ=√p2+q2sin(θ+α)
- Using the sine addition formula:
sin(θ+α)=sinθcosα+cosθsinα
- Substitute the values of cosα and sinα:
sin(θ+α)=sinθ(q√p2+q2)+cosθ(p√p2+q2)
- Now substituting this back into the sine rule equation:
AB=√p2+q2⋅sinθsinθ⋅q√p2+q2+cosθ⋅p√p2+q2
- Simplifying gives:
AB=(p2+q2)⋅sinθq⋅sinθ+p⋅cosθ
Thus, the length of AB is given by:
AB=p2+q2⋅sinθp⋅cosθ+q⋅sinθ
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (JEE Advanced)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Multiple correct Answer Type)4videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Numerical value type22videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, if AB=8,BC=6,AC=10andCD=9, then AD =
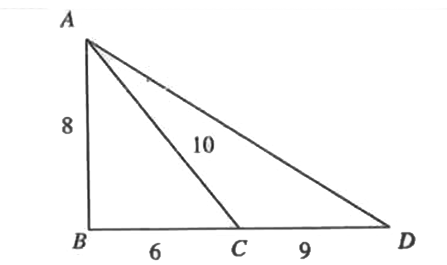 A12B13C15D17
A12B13C15D17 - Question 2 - Select One

If, in the figure above, CD=1, AB=-2, and AD=6, then BC=A5B9C2+√5D3√5
ABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionIf a,b,c,d are in H.P., then ab+bc+cd is equal to
View SolutionIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.View SolutionLet ABCD be a trapezium ,in which AB is parallel to CD, AB =11 ,BC=4,CD=6 and DA=3. the distance between AB and CD is
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View Solution
