Let ABCDEFGHIJKL be a regular dodecagon. Then the value of ABAF+AFAB is equal to ____
The correct Answer is:4
To solve the problem of finding the value of ABAF+AFAB for a regular dodecagon ABCDEFGHIJKL, we can follow these steps:
Step 1: Understand the Geometry of the Dodecagon
A regular dodecagon has 12 equal sides and is inscribed in a circle. The center of the dodecagon can be denoted as point O. The vertices are labeled as A, B, C, D, E, F, G, H, I, J, K, L in a clockwise manner.
Step 2: Determine the Lengths of AB and AF
1. Finding AB:
- The angle subtended by each side at the center (O) is 360∘12=30∘.
- The length AB can be calculated using the formula for the chord length in a circle:
AB=2Rsin(30∘2)=2Rsin(15∘)
2. Finding AF:
- The angle subtended by AF at the center is 150∘ (since A to F skips 5 vertices).
- The length AF can be calculated similarly:
AF=2Rsin(150∘2)=2Rsin(75∘)
Step 3: Substitute the Lengths into the Expression
Now we can substitute AB and AF into the expression:
ABAF+AFAB=2Rsin(15∘)2Rsin(75∘)+2Rsin(75∘)2Rsin(15∘)
This simplifies to:
sin(15∘)sin(75∘)+sin(75∘)sin(15∘)
Step 4: Use the Identity for Sine
Recall that sin(75∘)=cos(15∘). Therefore, we can rewrite the expression as:
sin(15∘)cos(15∘)+cos(15∘)sin(15∘)=tan(15∘)+cot(15∘)
Step 5: Simplify the Expression
Using the identity tan(x)+cot(x)=sin2(x)+cos2(x)sin(x)cos(x)=1sin(x)cos(x):
tan(15∘)+cot(15∘)=1sin(15∘)cos(15∘)=2sin(30∘)=4
Final Answer
Thus, the value of ABAF+AFAB is equal to 4.
---
A regular dodecagon has 12 equal sides and is inscribed in a circle. The center of the dodecagon can be denoted as point O. The vertices are labeled as A, B, C, D, E, F, G, H, I, J, K, L in a clockwise manner.
1. Finding AB:
- The angle subtended by each side at the center (O) is 360∘12=30∘.
- The length AB can be calculated using the formula for the chord length in a circle:
AB=2Rsin(30∘2)=2Rsin(15∘)
- The angle subtended by AF at the center is 150∘ (since A to F skips 5 vertices).
- The length AF can be calculated similarly:
AF=2Rsin(150∘2)=2Rsin(75∘)
Now we can substitute AB and AF into the expression:
ABAF+AFAB=2Rsin(15∘)2Rsin(75∘)+2Rsin(75∘)2Rsin(15∘)
This simplifies to:
sin(15∘)sin(75∘)+sin(75∘)sin(15∘)
Recall that sin(75∘)=cos(15∘). Therefore, we can rewrite the expression as:
sin(15∘)cos(15∘)+cos(15∘)sin(15∘)=tan(15∘)+cot(15∘)
Using the identity tan(x)+cot(x)=sin2(x)+cos2(x)sin(x)cos(x)=1sin(x)cos(x):
tan(15∘)+cot(15∘)=1sin(15∘)cos(15∘)=2sin(30∘)=4
Thus, the value of ABAF+AFAB is equal to 4.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Single correct Answer type)
2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (JEE Advanced)
3 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Matrix match type
6 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
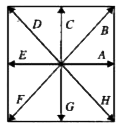
A number of vectors are as shown in .They can be combined in various ways , like →A+→C=→B . What is the value of (a) →E+→C (b) →A+→F (c ) →A+→D (d) →E+→A (e ) →A−→B .
View SolutionIf ABCDEF is a regular hexagon, prove that AD+EB+FC=4AB.
View SolutionLet ab=1, then the minimum value of 1a4+14b4 is
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to
View SolutionIf ABCDEF is a regular hexagon with −−→AB=→a and −−→BC=→b, then −−→CE equals
View SolutionIf a+b=7 and ab=12 find the value of a2−ab+b2.
View SolutionThe value of logab−log|b|=
View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionIn a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
View SolutionIf loga(ab)=x then logb(ab) is equals to
View Solution
