If I1,I2,I3 are the centers of escribed circles of ΔABC, show that the area of ΔI1I2I3 is (abc)/(2r)
Area =I1I2×I3I2×I1I34R'
where R' = Circumradius of ΔI1I2I3
=(4Rcos.A2)(4Rcos.B2)(4Rcos.C2)8R (∵ΔABC is pedal triangle for ΔI1,I2,I3)
=8R2cos.A2cos.B2cos.C2
=R2sinAsinBsinCsin.A2sin.B2sin.C2
=R2abc8R3sin.A2sin.B2sin.C2
=abc2(4Rsin.A2sin.B2sin.C2)
=abc2r
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.1
12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.2
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Knowledge Check
In the circuit shown, the value of currents I1,I2andI3 are
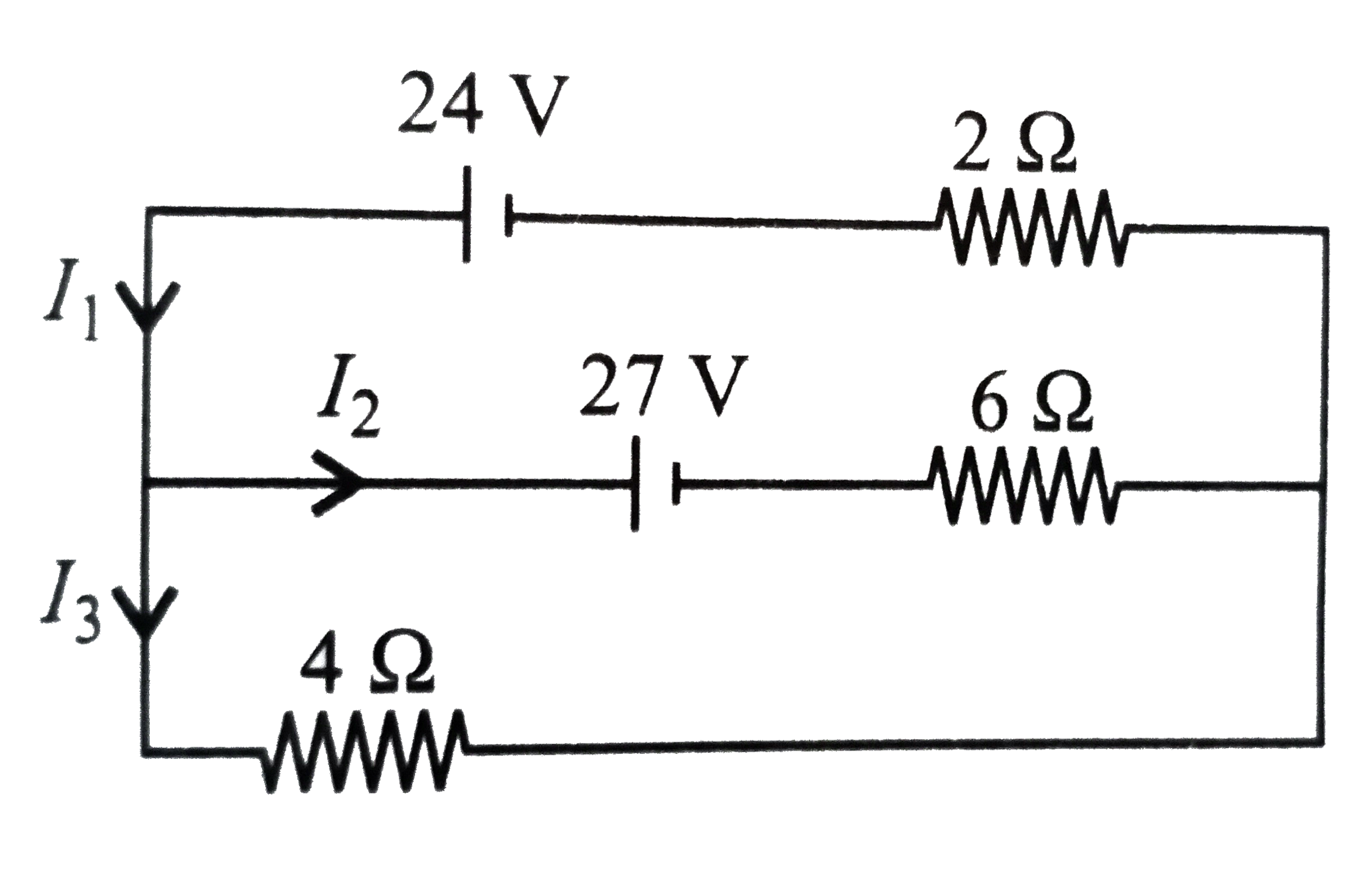 A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
If I is the incentre and I1,I2,I3 are the centre of escribed circles of the △ABC. Prove that
II1.II2.II3=16R2r.
View SolutionThe radii r1,r2,r3 of the escribed circles of the triangle ABC are in H.P. If the area of the triangle is 24cm2 and its perimeter is 24 cm, then the length of its largest side is
View SolutionIf I1 is the centre of the escribed circle touching side BC of !ABC in which ∠A=60∘, then I1 A =
View SolutionIf I is the incenter of ΔABCandR1,R2,andR3 are, respectively, the radii of the circumcircle of the triangle IBC, ICA, and IAB, then prove that R1R2R3=2rR2
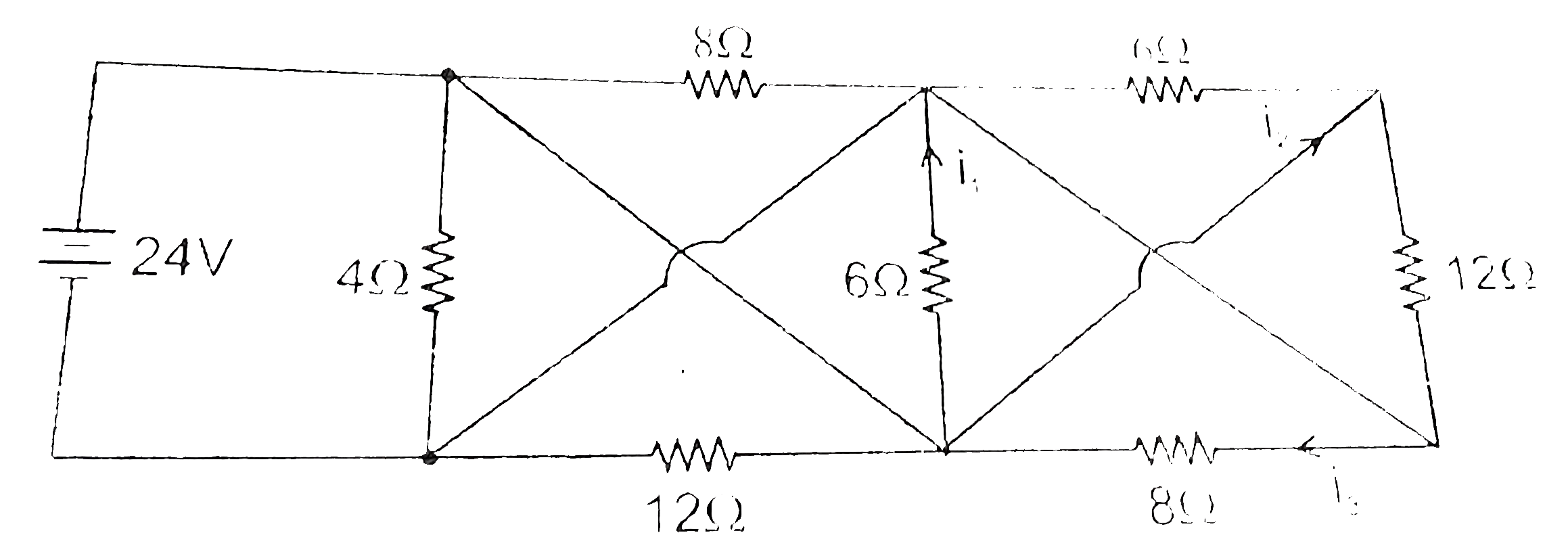
View SolutionCalculate ratio of i1 and (i2+i3)
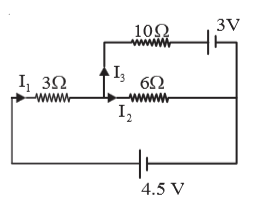
View SolutionFind the current I1, I2, & I3, in the circuit.
View SolutionIf z1,z2,z3 are the vertices of an equilational triangle ABC such that |z1−i|=|z2−i|=|z3−i|, then |z1+z2+z3| equals to
View Solution
