In a ΔABC, the median to the side BC is of length 1√11−6√3 and it divides the ∠A into angles 30∘ and 45∘. Find the length of the side BC.
To solve the problem step by step, we will use the information given in the question about triangle ABC and the properties of medians and angles.
Step 1: Understand the Triangle and Given Information
We have triangle ABC with median AD to side BC. The length of median AD is given as 1√11−6√3. The median divides angle A into two angles: 30∘ and 45∘.
Step 2: Define the Length of Side BC
Let the length of side BC be a. Since D is the midpoint of BC, we have BD=DC=a2.
Step 3: Apply the Angle Bisector Theorem
According to the angle bisector theorem, we can express the cotangent of angle A using the segments created by the median:
m+ncotθ=mcotα−ncotβ
where m=BD=a2, n=DC=a2, α=30∘, β=45∘, and θ=75∘ (since 30∘+45∘=75∘).
Step 4: Calculate Cotangents
Now, we calculate the cotangents:
- cot(30∘)=√3
- cot(45∘)=1
Substituting these values into the equation:
a2+a2cot(75∘)=a2√3−a2
This simplifies to:
acot(75∘)=a(√3−1)
Thus,
cot(75∘)=√3−1
Step 5: Use the Median Length Formula
The length of the median AD can also be expressed using the formula:
AD=12√2AB2+2AC2−BC2
However, we can use the given length of the median:
AD=1√11−6√3
Step 6: Set Up the Equation
Equating the two expressions for AD:
1√11−6√3=a2√2⋅sin(75∘)
Using sin(75∘)=sin(30∘+45∘)=√6+√24:
1√11−6√3=a2√2⋅√6+√24
Step 7: Solve for a
Cross-multiplying to solve for a:
2√2=a⋅√6+√24√11−6√3
Rearranging gives:
a=8√2(√6+√2)√11−6√3
Step 8: Simplifying the Expression
After simplifying the expression, we find that a=2.
Conclusion
Thus, the length of side BC is 2.
We have triangle ABC with median AD to side BC. The length of median AD is given as 1√11−6√3. The median divides angle A into two angles: 30∘ and 45∘.
Let the length of side BC be a. Since D is the midpoint of BC, we have BD=DC=a2.
According to the angle bisector theorem, we can express the cotangent of angle A using the segments created by the median:
m+ncotθ=mcotα−ncotβ
where m=BD=a2, n=DC=a2, α=30∘, β=45∘, and θ=75∘ (since 30∘+45∘=75∘).
Now, we calculate the cotangents:
- cot(30∘)=√3
- cot(45∘)=1
a2+a2cot(75∘)=a2√3−a2
This simplifies to:
acot(75∘)=a(√3−1)
Thus,
cot(75∘)=√3−1
The length of the median AD can also be expressed using the formula:
AD=12√2AB2+2AC2−BC2
However, we can use the given length of the median:
AD=1√11−6√3
Equating the two expressions for AD:
1√11−6√3=a2√2⋅sin(75∘)
Using sin(75∘)=sin(30∘+45∘)=√6+√24:
1√11−6√3=a2√2⋅√6+√24
Cross-multiplying to solve for a:
2√2=a⋅√6+√24√11−6√3
Rearranging gives:
a=8√2(√6+√2)√11−6√3
After simplifying the expression, we find that a=2.
Thus, the length of side BC is 2.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Illustration
86 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.1
12 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
In a ΔABC if the length of the sides are √2,√6 and √8, then the measures of the angles are
View SolutionWhat is the length of side BC in Figure ?
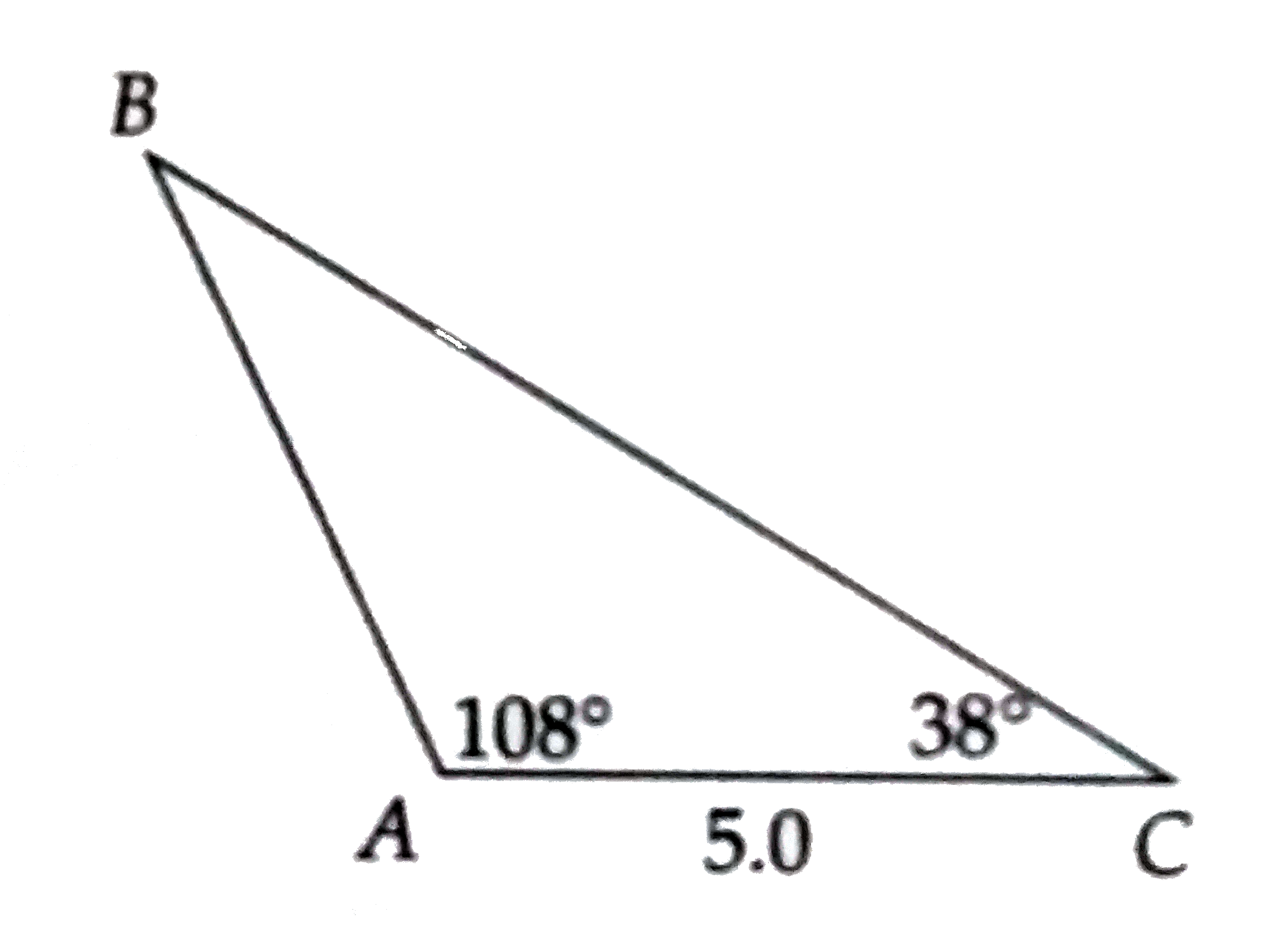
View SolutionIn triangle ABC,AB=6,AC=3√6,∠B=60∘ and ∠C=45∘. Find length of side BC.
View SolutionIn a !ABC the length of the median AD to the side BC is 4 units. If ∠A=60∘ and the area of the triangle is 2√3 sq. units. The length of side BC, is
View SolutionIn ΔABC, angle A is 120∘,BC+CA=20,andAB+BC=21 Find the length of the side BC
View Solution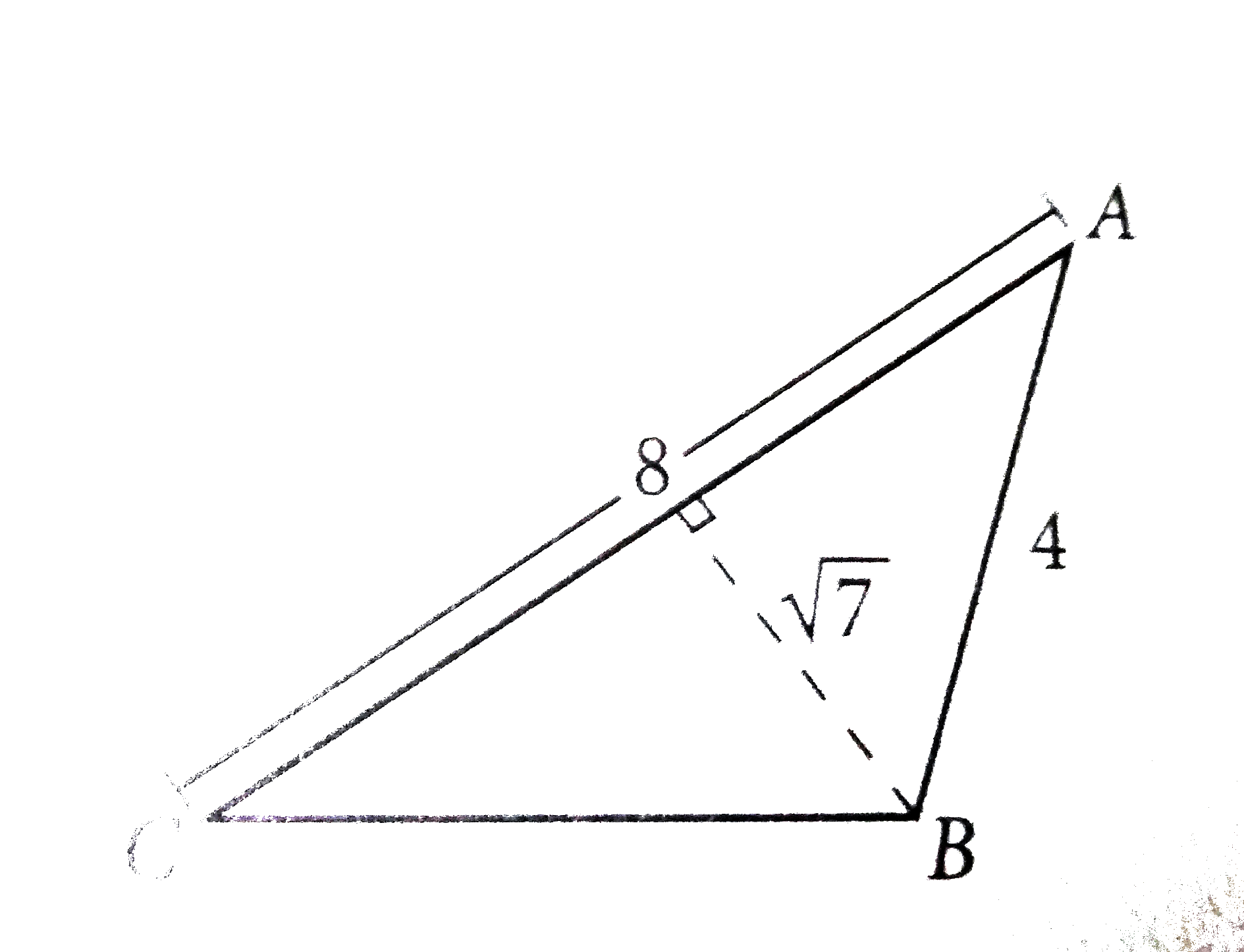
In the figure above, what is the length of side BC?
View SolutionFind the length of side BC in the given triangle.
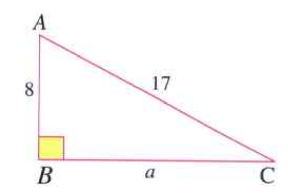
View SolutionIn a triangle ABC, right-angled at B, side BC = 20 cm and angle A= 30°. Find the length of AB.
View SolutionTwo sides of a triangle are of lengths √6and4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area.
View SolutionIn ΔABC,
if the sides are 7,4√3and√13 cm, prove that the smallest angle is 30∘.
View Solution
