If ∫x2−x+1(x2+1)32exdx=exf(x)+c, then (a) f(x) is an even function (b) f(x) is a bounded function (c) the range of f(x) is (0,1) (d) f(x) has two points of extrema
f(x) is an even function
f(x) is a bounded function
the range of f(x) is (0, 1]
f(x) has two points of extrema
The correct Answer is:A, B, C
I=∫x2−x+1(x2+1)3/2exdx
=∫ex[x2+1(x2+1)3/2−x(x2+1)3/2]dx
=∫ex[1√x2+1+{−x(x2+1)3/2}]dx
=ex[f(x)+f'(x)]dx, where f(x)=1√x2+1
=exf(x)+c=ex√x2+1+c
The graph of f(x) is given in the figure.
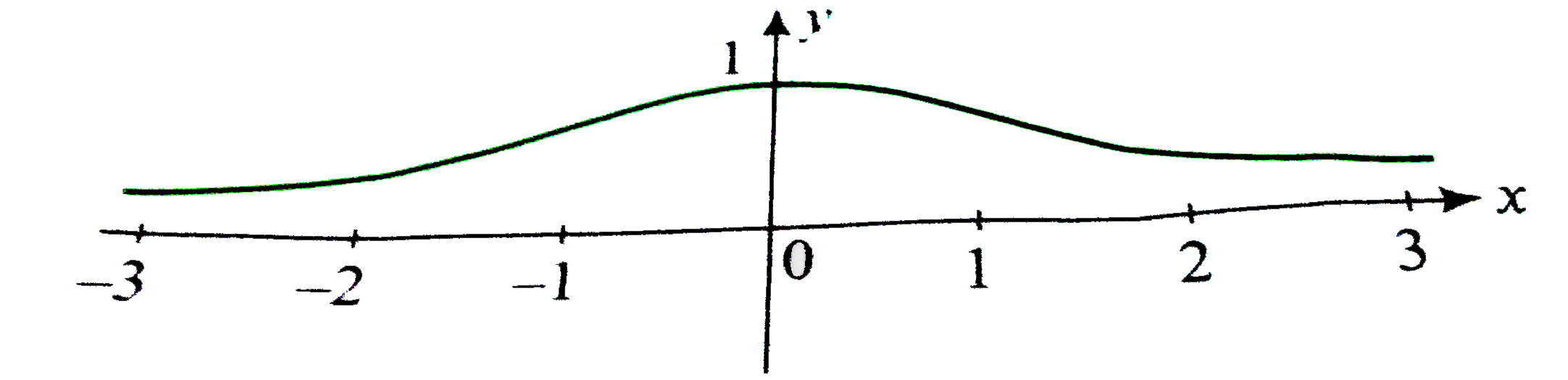
From the graph, f(x) is even, bounded function and has the range (0, 1].
Topper's Solved these Questions
- INDEFINITE INTEGRATIONBOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercises (Linked Comprehension Type)
17 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISES (Matrix Match Type)
4 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISES (Single Correct Answer Type)
77 Videos
- HYPERBOLABOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
- INEQUALITIES AND MODULUSBOOK - CENGAGE ENGLISHCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer
21 Videos
Similar Questions
If ∫(x−1x2)exdx=f(x)ex+c, then write the value of f(x).
View SolutionIf ∫(x−1x2)ex dx=f(x) ex+C, then write the value of f(x) .
View Solution∫x+1x(1+xex)2dx=log|1−f(x)|+f(x)+c, then f(x)=
View SolutionIf ∫ex−1ex+1dx=f(x)+C, then f(x) is equal to
View SolutionGiven ∫ex (tanx+1)secx dx=exf(x)+c, write f(x) satisfying the above.
View SolutionLet f(x) be a continuous function in R such that f(x) does not vanish for all x∈R. If ∫51f(x)dx=∫5−1f(x)dx, then in R,f(x) is (A) an even function (B) an odd function (C) a periodic function with period 5 (D) none of these
View SolutionIf ∫dxx2+ax+1=f(g(x))+c, then f(x) is inverse trigonometric function for |a|>2 f(x) is logarithmic function for |a|<2 g(x) is quadratic function for |a|>2 g(x) is rational function for |a|<2
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionEvaluate: ∫ex(f(x)+f′(x))dx=exf(x)+C
View Solution
