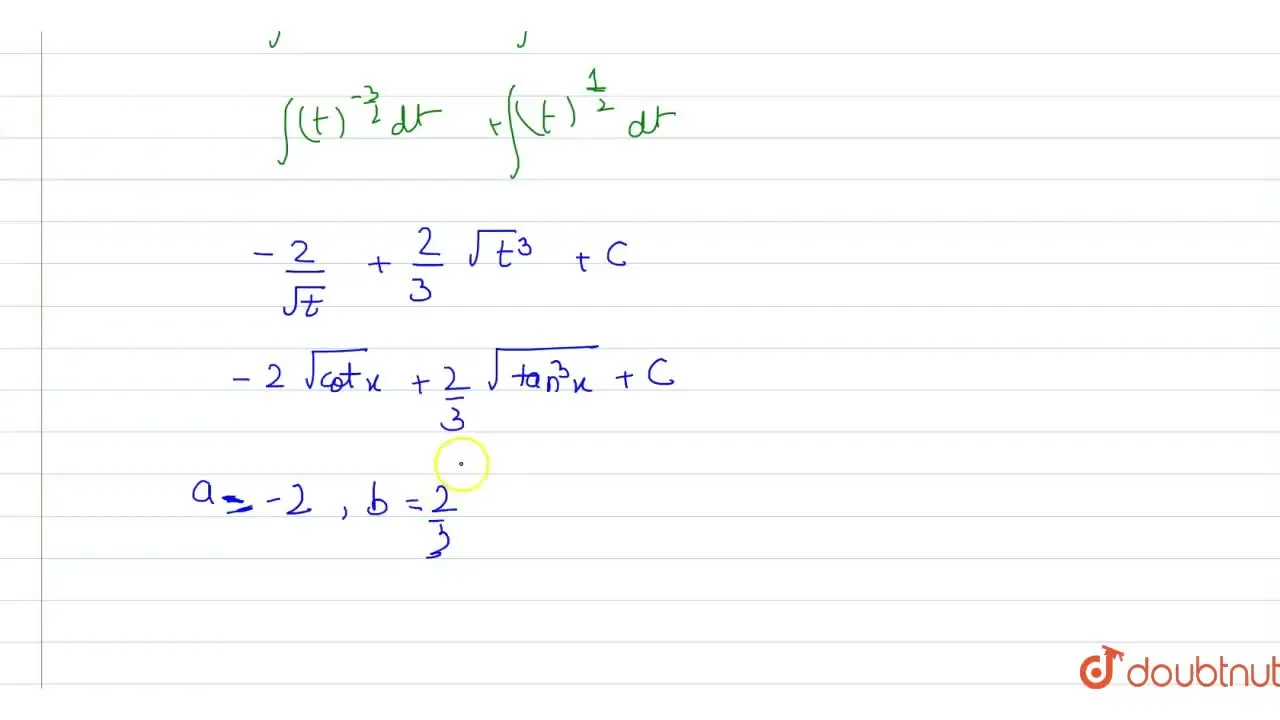If ∫dx√sin3xcos5x=a√cotx+b√tan3x+c, then
A
a=−1,b=1/3
B
a=−3,b=2/3
C
a=−2,b=4/3
D
a=−2,b=2/3
Video Solution
Text Solution
The correct Answer is:D
I=∫dx√sin3xcos5x
=∫dx√sin3xcos3xcos8x
=∫sec4x√tan3xdx
=∫(1+tan2x)sec2x√tan3xdx
Let t=tanx or dt=sec2xdx
∴I=∫1+t2t3/2dt
=∫(t−3/2+t1/2)dt
=−2t−12+23t3/2+C
=−2√cotx+23√tan3x+C
∴a=−2,b=23
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercises (Multiple Correct Answers Type)17videos
INDEFINITE INTEGRATION
- BOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercises (Linked Comprehension Type)17videos
INDEFINITE INTEGRATION
- BOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - CONCEPT APPLICATION EXERCISE 7.915videos
INDEFINITE INTEGRATION
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
Similar Questions
If ∫dx√sin3xcos5x=a√cotx+b√tan3x+c, then (a)a=−1,b=13 (b) a=−3,b=23 (c)a=−2,b=43 (d) none of these
View Solution∫1√sin3xcosxdx=?
View Solution∫5x−2√3x+7dx
View Solution∫1√tanxdx
View SolutionEvaluate: ∫1√sin3xcos5x dx
View Solution∫dx√cos3xcos(x−α) is equal to
View Solution∫cosec2x.√cotdx
View Solution∫(x−3)2√xdx
View SolutionI f∫dxcos3x√sin2x=a(tan2x+b)√tanx+c
View Solution∫1√sin3xsin(x+α)dx is equal to
View Solution