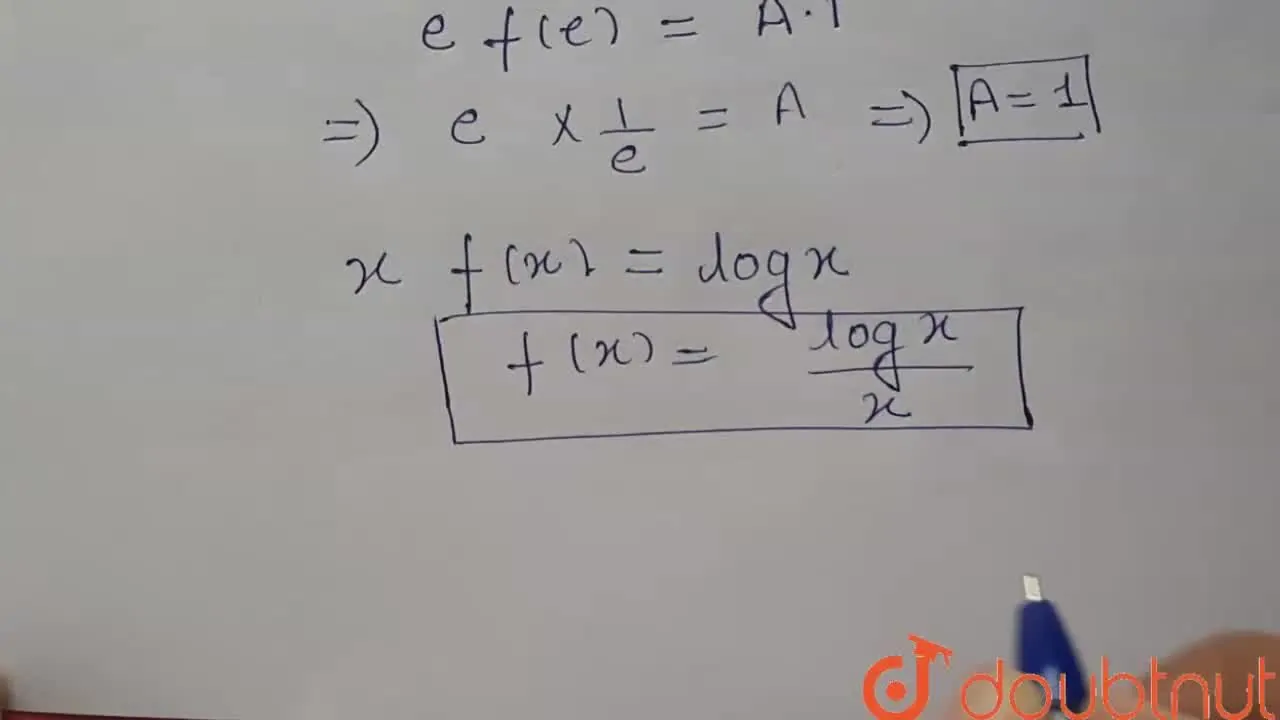If f(x)=f(x)y+f(y)x holds for all real x and y greater than 0andf(x) is a differentiable function for all x>0 such that f(e)=1e,thenf∈df(x).
We have
f(xy)=f(x)y+f(y)x for all x,y>0
or f(1)=f(1)+f(1) [Putting x=y=1]
or f(1)=0
Now, f(x) is differentiable for all x >0. Therefore,
f'(x)=limh→0f(x+h)−f(x)h
=limh→0f{x(1+hx)}−f(x)h
=limh→0f(x)1+hx+f(1+hx)x−f(x)h
=limh→0−hxf(x)1+hx+f(1+hx)xh
=−f(x)x+limh→0f(1+hx)hx
=−f(x)x+1x2limh→0f(1+hx)hx
=−f(x)x+Ax2, where A=limh→0f(1+hx)hx
∴ ddx(f(x))=−f(x)x=Ax2
or ddx(f(x))+f(x)x=Ax2
or xddx(f(x))+f(x)=Ax
or ddx[xf(x)]=Ax
or xf(x)=Alogex+logC [On integration]
Putting x=1, we get
f(1)=Aloge1+logC
or 0=logC [∵f(1)=0]
or xf(x)=Alogex
Putting x=e, we get
ef(e)=Alogee
or A=1 [∵f(e)=1e]
∴ xf(x)=logex
or f(x)logexx
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Concept Application 3.11videos
DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Concept Application 3.240videos
DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Archives14videos
DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type5videos
DIFFERENTIAL EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DOT PRODUCTEXERCISE - DPP 2.115videos
DOT PRODUCT
Similar Questions
If f(xy)=f(x)y+f(y)x holds for all real x and y greater than 0 and f(x) is a differentiable function for all x>0 such that f(e)=1e , then find f(x)
View SolutionIf f:R→R is a differentiable function such that f(x)>2f(x) for all x∈R and f(0)=1, then
View SolutionIf f is real-valued differentiable function such that f(x)f'(x)<0 for all real x, then
View SolutionIf f is real-valued differentiable function such that f(x)f'(x)<0 for all real x, then
View SolutionLet f(x+y)=f(x)+f(y)+2xy−1 for all real x and y and f(x) be a differentiable function. If f′(0)=cosα, the prove that f(x)>0∀x∈R.
View SolutionLet f(x+y)=f(x)+f(y)+2xy−1 for all real xandy and f(x) be a differentiable function. If f′(0)=cosα, the prove that f(x)>0∀x∈R.
View SolutionLet f(x+y)=f(x)+f(y)+2xy−1 for all real xandy and f(x) be a differentiable function. If f′(0)=cosα, the prove that f(x)>0∀x∈R.
View SolutionLet f(x+y)=f(x)+f(y)+2xy−1 for all real xandy and f(x) be a differentiable function. If f′(0)=cosα, the prove that f(x)>0∀x∈R.
View SolutionIf f(x+y3)=2+f(x)+f(y)3 for all real xandy and f′(2)=2, then determine y=f(x).
View SolutionIf f(x+y3)=2+f(x)+f(y)3 for all real xandy and f′(2)=2, then determine y=f(x).
View Solution