If P is any arbitary point on the circumcurcle of the equilateral triangle of side length l units, then is always equal to
The correct Answer is:a
Let P.V. of A,B and C be
respectively, and be the circumcentre of equilateral traingle ABC. Then
Now
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Reasoning type8videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Comprehension type27videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercises15videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTSEXERCISE - All Questions264videos
DETERMINANTS
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type5videos
DIFFERENTIAL EQUATIONS
Similar Questions
If P is any arbitrary point on the circumcircle of the equilateral triangle of side length l units, then ∣∣→PA∣∣2+∣∣→PB∣∣2+∣∣→PC∣∣2 is always equal to 2l2 b. 2√3l2 c. l2 d. 3l2
View SolutionIf P is any arbitrary point on the circumcirlce of the equllateral trangle of side length l units, then ∣∣→PA∣∣2+∣∣→PB∣∣2+∣∣→PC∣∣2 is always equal to 2l2 b. 2√3l2 c. l2 d. 3l2
View Solution
Knowledge Check
- Question 1 - Select One
If ∣∣→a×→b∣∣=4 and ∣∣→a.→b∣∣=2, then |→a|2∣∣→b∣∣2 is equal to
A6B8C20Dnone of these - Question 2 - Select One
if ∣∣→a×→b∣∣2+∣∣→a.→b∣∣2=144 and |→a|=4 then ∣∣→b∣∣ is equal to
A12B3C4D−3
ABC is an equilateral triangle of side 2m. If →E=10NC−1 then VA−VB is
 View Solution
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
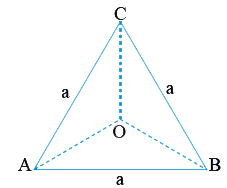
−−→AB+−−→BC+−−→CAView SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
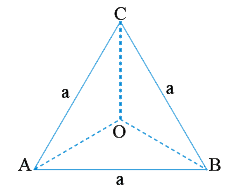
If ∣∣∣−−→AB+−−→BC+−−→AC∣∣∣=na then n = ?View SolutionIf P, Q , R are the mid-points of the sides AB, BC and CA of ΔABC and O is point whithin the triangle, then −−→OA+−−→OB+−−→OC=
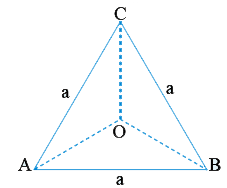
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
If −−→AB+−−→AC=n−−→AO then n = ?View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
View Solution
