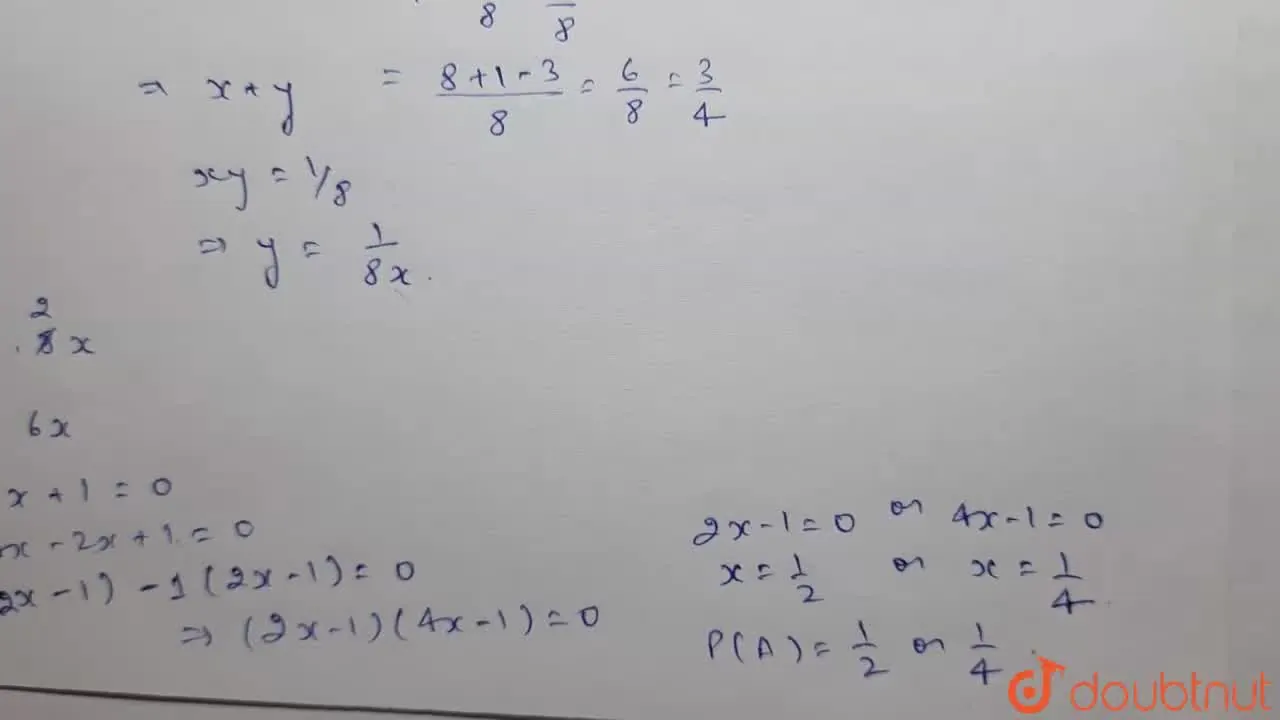If A and B are two independent events, the probability that both A and B occur is 1/8 are the probability that neither of them occours is 3/8. Find the probaility of the occurrence of A.
We have,
P(A∩B)=18andP(¯¯¯A∩¯¯¯B)=38
∴P(A)P(B)=18andP(¯¯¯A)P(¯¯¯B)=38
[∴A and B are independent]
Now, P(¯¯¯A∩¯¯¯B)=38
⇒1−P(A∩B)=38
or1−(P(A)+P(B)−P(A∩B))=38
or1−(P(A)+P(B))+18=38
orP(A)+P(B)=34
The equation whose roots are P(A) and P(B) is x2−x{P(A)+P(B)}+P(A)P(B)=0
orx2−34x+18=0
or8x2−6x+1=0
orx=12,14
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - SOLVED EXAMPLES21videos
PROBABILITY II
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - CONCEPT APPCICATION EXERCISE 14.15videos
PROBABILITY II
- BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - JEE Advanced7videos
PROBABILITY I
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
Similar Questions
A and B are two independent events.The probability that both A and B occur is 1/6 and the probability that neither of them occurs is 1/3.Then the probability of the two events are respectively:
View SolutionIf A and B are two independent events, then the probability that only one of A and B occur is
View SolutionE and F are two independent events. The probability that both e and F happen is 1/12 and the probability that neither E nor F happens is 1/2. Then
View SolutionLet A and B be two independent events. The probability of their simultaneous occurrence is 1/8 and the probability that neither occurs is 3/8. Find P(A)andP(B).
View SolutionLet A and B be two independent events. The probability of their simultaneous occurrence is 1/8 and the probability that neither occurs is 3/8. Find P(A)andP(B).
View SolutionThe probability of the occurrence of an event is 38. Find the probability of the non-occurrence of the event.
View SolutionGiven two independent events, if the probability that both the events occur is 849, the probability that exactly one of them occurs is 2649 and the probability of more probable of the two events is λ, then 14λ is equal to
View SolutionThe probability of the occurrence of an event is 37. Find the probability of the non occurrence of the event.
View SolutionGiven two independent events, if the probability that exactly one of them occurs is 26/49 and the probability that none of them occurs is 15/49, then the probability of more probable of two events is
View SolutionIf A and B are two events, the probability that exactly one of them occurs is given by
View Solution